1) Estudo dos gases perfeitos
2) As leis da Termodinâmica
Exercício 1:
(ITA-SP)
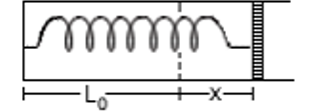
Um mol de gás perfeito está contido em um cilindro de secção S fechado por um pistão móvel, ligado a uma mola de constante elástica k. Inicialmente, o gás está na pressão atmosférica P0, temperatura T0, e o comprimento do trecho do cilindro ocupado pelo gás é L0, com a mola não estando deformada. O sistema gás-mola é aquecido e o pistão se desloca de uma distância x.
Denotando a constante de gás por R, a nova temperatura do gás é:
a) T0 + x/R(P0S + kL0)
b) T0 + L/R(P0S + kx)
c) T0 + x/R(P0S + kx)
d) T0 + kx/R(L0S + x)
e) T0 + x/R(P0S + kL0 + kx)
Resolução:
Equação de Clapeyron:
P0V0 = nRT0 => P0SL0 = nRT0 (1)
PV = nRT => (P0+kx/S).S(L0+x) = nRT =>
P0SL0 + kxL0 + P0Sx + kx2 = nRT (2)
De (1) em (2) e sendo n = 1 mol, temos:
RT0 + kxL0 + P0Sx + kx2 = RT => T = T0 + x/R(P0S + kL0 + kx)
Resposta: e
Exercício 2:
(UFTM-MG)
A figura representa, esquematicamente, uma máquina térmica que trabalha em ciclos, concebida para transformar a energia térmica, recebida de uma fonte onde se queima determinado combustível, em trabalho mecânico útil.
Nessa máquina, um gás ideal sofre, a cada ciclo, a transformação ABCA, representada no diagrama P x V, e o calor não aproveitado é absorvido por um sistema de refrigeração e retirado da máquina.
a) Calcule o trabalho mecânico útil realizado pela máquina a cada ciclo.
b) Sabendo que o número de mols de gás na máquina é constante e que sua temperatura no estado A é de 400 K, quais serão as temperaturas nos estados
B e C?
Resolução:
a)
O trabalho é numericamente igual à área do ciclo (área do triângulo):
τ = (base x altura)/2 (numericamente)
τ = (3-2).10-2m3.(6-4).104(N/m2)/2 => τ = 102 J
b)
PAVA/TA = PBVB/TB => 4.104.2.10-2/400 = 6.104.2.10-2/TB => TB = 600 J
PBVB/TB = PCVC/TC => 6.104.2.10-2/600 = 4.104.3.10-2/TC => TC = 600 J
Respostas:
a) 100 J
b) 600 K e 600 K
Próxima semana:
1) Primeira Lei da Termodinâmica
2) Segunda Lei da Termodinâmica


Nenhum comentário:
Postar um comentário