Dica do Blog

Clique para ampliar

Eclipse na praia

x

Na foto o eclipse solar total de 11 de julho, visto da praia de Anakena Beach, na Ilha de Páscoa.

x

Clique aqui e veja mais fotos de astronomia.

Mecânica

Clique para ampliar

x

Aplicação da 2ª Lei de Newton
x

Borges e Nicolau
No quadro acima temos um plano inclinado deslocando-se para a direita com aceleração constante. O movimento é horizontal. Apoiada no plano há uma bolinha em repouso em relação a ele. Não há atritos.

Vamos estudar como se relacionam as forças que atuam na bolinha.
Há duas interações notáveis, bolinha/Terra (interação de campo) e bolinha/plano, (interação de contato).

Na figura 1 temos a interação de campo representada pela força peso (P), que é representada por um vetor de direção vertical e sentido para baixo. O módulo do vetor peso é dado por (P = m.g), onde m é a massa do corpo que interage com a Terra e g a aceleração da gravidade local.

Na figura 2 temos a interação de contato bolinha/plano, representada pela força normal (FN), que é um vetor com direção perpendicular à superfície de contato e sentido de afastamento do contato.

x
Na figura 3 temos a resultante (FR) dos vetores peso e normal (FN).

Como a bolinha descreve um MRUV horizontal, o vetor que representa a resultante FR tem direção horizontal.

Clique para ampliar

Relações matemáticas

Na figura 4 temos dois ângulos de lados perpendiculares, portanto iguais. Nas figuras 5 e 6 o triângulo de forças está configurado com os vetores FN e P colocados de forma consecutiva e, a resultante FR, com a origem na origem do segmento orientado que representa o primeiro (FN) e a extremidade na extermidade do segundo (P).

Clique para ampliar

Desafio de Mestre

Clique para ampliar

Plano Inclinado

Borges e Nicolau
Para colocar uma caixa de massa igual a 200 kg na carroceria de um caminhão, Seu Joaquim adapta um plano inclinado que forma com a horizontal um ângulo θ; tal que sen θ = 0,60 e cos θ = 0,80. Por meio de uma corda inextensível puxa o carrinho que transporta a caixa. Considere a massa do carrinho igual a 20 kg.

Se o carrinho sobe em MRU, qual é a intensidade da força de tração na corda?

Depois de descarregar a caixa o carrinho desce vazio o plano inclinado, mas também em MRU.

Qual é a nova intensidade da força de tração na corda?

Despreze o atrito do carrinho com o plano inclinado.

Considere g = 10 m/s².

Leituras do Blog

As estações do ano

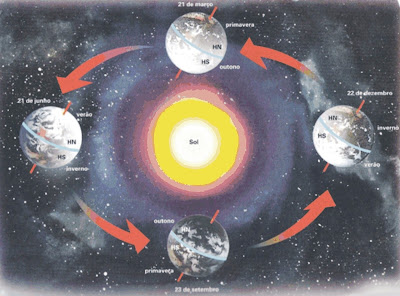
O eixo em torno do qual a Terra realiza seu movimento de rotação não é perpendicular ao plano de sua órbita em torno do Sol, mas apresenta uma inclinação de 23º 27' 30''.

Clique para ampliar

x

Devido a essa inclinação ocorrem as quatro estações do ano. Na ilustração temos as quatro posições da Terra que indicam o início de cada estação.

Clique para ampliar

x

Em 21 de junho inicia-se o verão no hemisfério norte e o inverno no hemisfério sul. Observe que o hemisfério norte se inclina para o Sol. Em 22 de dezembro inicia-se o verão no hemisfério sul e o inverno no hemisfério norte. Agora é o hemisfério sul que se inclina para o Sol.

x

Essas datas, que marcam o início das estações de inverno e verão, são denominadas solstícios.

x

A primavera e o outono começam nos equinócios: 21 de março _ primavera no hemisfério norte e outono no hemisfério sul; 23 de setembro – primavera no hemisfério sul e outono no hemisfério norte.

x

Nos equinócios, a duração do dia é igual à da noite. Devido à inclinação da Terra, as noites de inverno são mais longas do que as de verão. A noite mais longa é a do solstício de inverno (21 de junho no hemisfério Sul).

x

(Fonte: Os movimentos – pequena abordagem sobre Mecânica- de Nicolau Gilberto Ferraro)

X

Resposta da questão de 28 / 07

x

Exercício 10) A

Questões da IJSO

As estações do ano

10) Em qual dos casos, as diferentes estações do ano não serão observadas em um planeta?

(A) Quando o eixo de rotação do planeta está perpendicular ao plano orbital.

(B) Quando o eixo de rotação do planeta forma um ângulo obtuso com seu plano orbital.

(C) Quando o eixo de rotação do planeta está paralelo ao plano orbital.

(D) Quando o planeta segue uma órbita elíptica.


Resposta das questões de 27 / 07

Exercício 8) A

Exercício 9) C

Questões da IJSO

Eletrodinâmica

9) Um estudante fez algumas medidas acerca de um circuito elétrico com a ajuda dos seguintes dispositivos: uma bateria(1); caixa de resistores(2), interruptor (3), amperímetro(4), e voltímetro(5). De acordo com as indicações mostradas na figura abaixo, determine a força eletromotriz da bateria. As leituras do amperímetro são em ampères e do voltímetro em volts. Considere o amperímetro e o voltímetro ideais.

Clique para ampliar

(A) ε = 2.9 xxxxx(B) ε = 3.4 xxxxx(C) ε = 3.8 xxxxx(D) ε = 5.8

Questões da IJSO

Eletrodinâmica


8) Um anel de raio R, feito com material de resistividade ρ, é conectado ao circuito mostrado na figura acima. O ponto A está fixo, entretanto, o ponto B pode se mover de tal modo que o ângulo α varie, considere os elementos do circuito ideais. Qual dos gráficos abaixo nos fornece a indicação do amperímetro em função do ângulo α?

Clique para ampliar

x

Resposta das questões de 26 / 07

x

Exercício 6) C

x

Exercício 7) C

Questões da IJSO

Óptica Geométrica

7) Qual a trajetória descrita pelo raio de luz antes de deixar o prisma triangular que tem índice de refração n = 2,5? Sabe-se que o ângulo de incidência com a face do prisma é φ= 70º e o prisma está imerso no ar.

Nota: Na resolução deste exercício é permitido o uso de calculadora e tabela de senos.

Questões da IJSO

Termologia

6) Dois objetos de mesma massa têm a razão de seus calores específicos C1/C2 = 4/5. Um aquecedor pode elevar a temperatura do primeiro objeto provocando uma diferença de temperatura ΔT em 20 min. Quanto tempo leva para o mesmo aquecedor provocar uma diferença de temperatude de 3 ΔT no segundo objeto? (As perdas de calor podem ser desprezadas).

(A) 45 min xxxxx(B) 60 min xxxxx(C) 75 min xxxxx(D) 90 min

Resposta da questão de 25 / 07

Exercício 5) C

Questões da IJSO

Mecânica

5) Quando uma placa pentagonal PQRST é dependurada através dos pontos X e Y, as configurações de equilíbrio são mostradas nas figuras 1 e 2. Então, a placa é dependurada por meio dos pontos P, Q, R, S e T respectivamente. Qual das seguintes respostas está correta? (As secções são de formato quadrado).

Clique para ampliar
Clique para ampliar

Resposta da questão de 24 / 07

x

Exercício 4) D

Questões da IJSO

Mecânica

4) Uma bola que se move com velocidade u, colide elasticamente com um grande caminhão que se move com velocidade V na mesma direção e sentido oposto. Com que velocidade relativa ao solo a bola se moverá após a colisão? (Todas as velocidades são em relação ao solo).

(A) 2u+V xxxxx(B) u+V xxxxx(C) 2u+2V xxxxx(D) u+2V

Resposta da questão de 23 / 07

Exercício 3) B

Questões da IJSO

Mecânica

3) Um garoto está se movendo com o dobro da velocidade de um carrinho na mesma direção e sentido que este. Quando o garoto sobe no carrinho, a velocidade do carrinho é aumentada em 20%. Qual a razão entre as massas do carrinho e do garoto, respectivamente?

(A) 5 xxxxx(B) 4 xxxxx(C) 3 xxxxx(D) 2


Resposta das questões de 22 / 07

Exercício 1) B
Exercício 2) D

IJSO

Olimpíada

Borges e Nicolau
A IJSO Brasil é a etapa nacional da Olimpíada Internacional Júnior de Ciências, uma das maiores e mais importantes olimpíadas acadêmicas do planeta.

A fase regional foi realizada no dia 26 de junho (nas escolas inscritas) e a fase nacional ocorrerá no dia 21 de agosto (na Escola Politécnica da USP).

A fase internacional da IJSO será realizada em dezembro de 2010 na cidade de Abuja, na Nigéria, e deve contar com a participação de mais de 50 países.

No ano de 2009 a fase internacional foi realizada na cidade de Baku no Azerbaijão. Segundo os líderes do Brasil, os professores Ronaldo Fogo, Felipe Pereira e Allison Hirata, o nível de exigência e rigor nas provas no Azerbaijão foi mais alto que o da edição anterior, o que mostra que a Olimpíada está cada vez mais competitiva. Eles foram responsáveis pela discussão e tradução dos problemas apresentados, acompanhados do Professor Rawlinson Ibiapina.

Para você treinar vamos apresentar questões da prova de testes da fase internacional de 2009.

Questões da IJSO

Mecânica

x

1) Um objeto com velocidade inicial V0 e uma aceleração a, percorre uma distância L1. A partir daí começa a desacelerar com uma aceleração de mesmo módulo a, e para após percorrer uma nova distância L2. Se a razão L2 /L1 = k, qual é o máximo valor da velocidade do objeto durante seu deslocamento?

A) (k-1/k+1).V0
B) √(k/k-1).V0
C) (k/k-1).V0
D) √(k+1/k).V0

2) O objeto mostrado na figura 1 desliza pelos planos inclinados AB e BC os quais têm coeficiente de atrito µ = 0,4. O gráfico da velocidade em função do tempo é mostrado na figura 2. Qual é o ângulo formado entre a superfície horizontal e o plano BC? (g = 9,81 m/s²)

Clique para ampliar

(A) 34,3º xxxxx(B) 31,4º xxxxx(C) 30,8º xxxxx(D) 28,6º

Nota: Na resolução deste exercício é permitido o uso de calculadora e tabela de senos.

Resolução do Desafio de Mestre de 20 / 07

Trajetória de uma partícula eletrizada

Na primeira situação a trajetória é circular. Logo, o campo é magnético. Como a partícula está eletrizada positivamente e é desviada para cima concluímos, pela regra da mão esquerda (ou regra da mão direita número 2) que o campo B tem direção perpendicular à velocidade v e sentido do leitor para o papel.

Na segunda situação a trajetória é parabólica. Logo, o campo é elétrico. Como a partícula está eletrizada positivamente e é desviada para cima concluímos que o campo E tem direção perpendicular a v e sentido para cima.

Todas as afirmações estão erradas.

Resposta: E

Nota: Em negrito: vetor

Desafio de Mestre

Trajetória de uma partícula eletrizada

Borges e Nicolau
Uma partícula eletrizada com carga elétrica q > 0 desloca-se em movimento retilíneo e uniforme, com velocidade de módulo v. Num certo instante ela penetra numa região R onde existe um campo uniforme, que pode ser elétrico ou magnético. Duas situações são apresentadas: na primeira a partícula descreve um arco de circunferência e na segunda um ramo de parábola.

Clique para ampliar

Analise as afirmações seguintes:

I) Na primeira situação o campo é magnético, tem direção perpendicular à velocidade v e sentido do papel para o leitor.

II) Na primeira situação o campo é elétrico, tem direção perpendicular à velocidade v e sentido do leitor para o papel.

III) Na segunda situação o campo é magnético, tem direção e sentido da velocidade v.

IV) Na segunda situação o campo é elétrico, tem direção perpendicular à velocidade v e sentido para baixo.

Tem-se:

a) Somente I) e III) são corretas

b) Somente I) e IV) são corretas

c) Somente I) e II) são corretas

d) Todas as afirmações são corretas

e) Todas as afirmações estão erradas.

Nota: Em negrito: vetor.

Resolução do Desafio de Mestre de 18 / 07

Força magnética

O vetor B, resultante entre os vetores B1 e B2, deve ter a mesma direção da velocidade v com que a partícula foi lançada.

Assim, temos: tgθ = B2/B1 = > B2 = B1.tgθ

Resposta: C

Nota: Em negrito: vetor

Desafio de Mestre

Clique para ampliar

Força magnética

Borges e Nicolau
Uma partícula eletrizada é lançada com velocidade v, numa direção que forma um ângulo θ com o eixo Ox de um sistema cartesiano ortogonal xOy. Na região existe um campo magnético uniforme de intensidade B1, direção e sentido do eixo Ox. Além deste campo existe na região outro campo magnético uniforme de intensidade B2, direção e sentido de Oy.

Para que a força magnética resultante sobre a partícula seja nula a relação entre B1 e B2 é dada por:

a) B2 = B1 . senθ

b) B2 = B1 . cosθ

c) B2 = B1 . tgθ

d) B2 = B1

e) B2 = B1 . √2

Nota: Em negrito: vetor.

Resolução do Desafio de Mestre de 16 / 07

Lançamentos oblíquos

Pedra 1:

y = v0 . senθ. t + gt²/2 = > 2,0 = 3,0 . t + 5,0 . t² = > t = 0,40s

x1 = v0 . cosθ . t = > x1 = 4,0 . 0,40(m) = 1,6 m

Pedra 2:

y = - v0 . senθ. t + gt²/2 = > 2,0 = - 3,0 . t + 5,0 . t² = > t = 1,0s

x2 = v0 . cosθ . t = > x2 = 4,0 . 1,0(m) = 4,0 m

Δt = 1,0s - 0,40s = 0,60s

Resposta: A

Desafio de Mestre

Clique para ampliar

Lançamentos oblíquos

Borges e Nicolau
Duas pedras (1 e 2) são lançadas de um local situado a uma altura
h = 2,0 m da superfície livre das águas de um lago, com mesma velocidade v0 = 5,0 m/s e com o mesmo ângulo θ com a horizontal, conforme indica a figura. Despreze a resistência do ar.

Considere g = 10m/s², sen θ = 0,6 e cos θ = 0,8.

As pedras 1 e 2 atingem o lago nos pontos M e N, respectivamente. Em relação ao sistema de coordenadas xOy, pode-se afirmar que as abscissas dos pontos M e N e a diferença entre os instantes em que as pedras atingem o lago são, respectivamente:

a) 1,6 m; 4,0 m; 0,60 s

b) 1,6 m; 4,0 m; 0 s

c) 2,0 m; 2,4 m; 0,80 s

d) 1,6 m; 3,2 m; 0,40 s

e) 1,6 m; 4,0 m; 1,0 s

Resolução do Desafio de Mestre de 14 / 07

Clique para ampliar

x
Na esfera agem três forças. Uma de campo, o peso P e duas de contato, a tração T no fio e a força FP, da interação com a parede.

Clique para ampliar

Para estudar o equilíbrio da esfera é conveniente decompor as forças nas direções (x) e (y).

Clique para ampliar

No eixo x: TX = > Tcos 30º = > TX = T√3/2

No eixo y: TY = > Tsen 30º = > TY = T/2

Clique para ampliar

No triângulo retângulo:

(FP)² = (Fat)² + (FN)² (1)

Do equilíbrio:

Resultante em x nula:

FN = TX
FN = T√3/2

Resultante em y nula:

P = TY + Fat
P = T/2 + Fat

Somatória dos momentos em reação ao ponto O nula:

T.R = Fat.R
T = Fat

Portanto:

P = T/2 + T
T = 2P/3

Fat = 2P/3 (2)

x

FN = T√3/2 = > FN = 2P/3.√3/2 = > FN = P√3/3 (3)

x

Substituindo-se (2) e (3) em (1) , vem:

x

(FP)² = (2P/3)² + (P√3/3)²

^x

FP = P√7/3

x

Resposta: D

Desafio de Mestre

Clique para ampliar

Estática

Borges e Nicolau
Uma esfera homogênea de peso P está em equilíbrio suspensa por meio de um fio inextensível e de peso desprezível e apoiada numa parede vertical, conforme indica a figura.

Dados: sen 30º = 1/2 e cos 30º = √3/2

A intensidade da força que a parede exerce na esfera é igual a:

a) P

b) P√3/3

c) P√5/3

d) P√7/3

e) 2P

Óptica

Resposta do Desafio de Mestre de 12/07

Aplicando a Equação de Gauss

Clique para ampliar

Ponto C : 1/f = 1/Pc + 1/Pc' = > 1/10 = 1/20 + 1/Pc' = > Pc' = 20 cm

Ponto E : 1/f = 1/PE + 1/PE’ = > 1/10 = 1/15 + 1/PE' = > PE' = 30 cm

Sendo CD = 5√2 cm; vem DE = 5,0 cm

D'E'/DE = PE'/PE = > D'E'/5,0 = 30/15 = > D'E' = 10 cm

Portanto: C'D' = 10√2 cm

Resposta: C

Desafio de Mestre

Aplicando a Equação de Gauss

Borges e Nicolau
Um pequeno lápis CD de comprimento 5,0 √2 cm está disposto, conforme a figura, diante de uma lente esférica convergente de distância focal
f = 10 cm. Considere válidas as condições de nitidez de Gauss.
O comprimento da imagem C’D’ é igual a:

a) 5,0 cm;

b) 10 cm;

c) 10 cm;

d) 20 cm;

e) 20 cm

Clique para ampliar

Eletrodinâmica

Respostas do Desafio de Mestre de 10/07

Fechando a chave

Estando a chave aberta ou fechada a tensão elétrica no resistor de resistência R1 é a mesma. Logo, a intensidade da corrente que o atravessa permanece constante.

RESPOSTA: C

Mudando a tensão

De P = U.i, sendo a mesma potência, o chuveiro submetido a uma maior tensão será percorrido por uma corrente elétrica de menor intensidade.

RESPOSTA: D

Desafio de Mestre

Fechando a chave

Borges e Nicolau
No circuito indicado na figura o gerador é ideal, R1 e R2 são dois resistores e Ch uma chave, inicialmente aberta. Os fios de ligação são considerados ideais. Fecha-se a chave Ch.

Clique para ampliar

a) A intensidade da corrente que percorre R1 aumenta.
b) A intensidade da corrente que percorre R1 diminui.
c) A intensidade da corrente que percorre R1 permanece constante.
d) A intensidade da corrente que percorre o gerador permanece constante
e) A intensidade da corrente que percorre o gerador diminui.


Mudando a tensão

Um eletricista substitui um chuveiro elétrico de uma residência que estava ligado em 127 V por outro, de mesma potência, mas ligado em 220 V. O novo chuveiro:

a) passará a consumir mais energia elétrica;
b) passará a consumir menos energia elétrica;
c) será percorrido por uma corrente elétrica de maior intensidade;
d) será percorrido por uma corrente elétrica de menor intensidade;
e) apresentará menor resistência elétrica.

Leituras do Blog

A piezoeletrização

Borges e Nicolau
Existem vários processos de eletrização de um corpo: eletrização por atrito, por contato e por indução. Vamos fazer algumas considerações sobre outro processo de eletrização: a piezoeletrização.

Certos cristais como, por exemplo, o quartzo e a turmalina, quando comprimidos, eletrizam suas faces opostas com cargas elétricas de sinais contrários. Este fenômeno foi descoberto, em 1880, pelos irmãos Pierre Curie (1859 – 1906) e Jacques Curie (1855 – 1941) e é denominado piezoeletrização.

Determinados materiais cerâmicos apresentam também o efeito piezoelétrico, como é o caso de titânio-zirconato de chumbo (PZT).

Reciprocamente, o cristal piezoelétrico flexiona quando se aplica uma tensão elétrica entre suas faces opostas. Nos fenômenos descritos se baseiam os funcionamentos dos microfones de cristal, de alguns acendedores de fogão (magiclick) e dos relógios de quartzo.

Para mais detalhes

Efeito piezoelétrico - Efeito piezo reverso - Geração de ultra-som. Clique aqui

Balada sustentável. Clique aqui e aqui

A piezoeletricidade. Clique aqui

Relógios de quartzo. Clique aqui

Microfone de cristal e de outros tipos. Clique aqui

Campo Elétrico

Clique para ampliar

Força atuando em uma carga de prova

Borges e Nicolau
No quadro acima temos um campo elétrico representado por linhas de força, que são linhas orientadas que partem de cargas positivas e chegam em cargas negativas. Essas linhas nunca se cruzam. Num ponto P qualquer de uma linha de força, o vetor campo elétrico tem a direção da reta tangente à linha e sentido coincidente com a orientação desta.

Colocando-se uma carga de prova q num ponto do campo, agirá sobre ela uma força de natureza eletrostática, tal que:

No quadro abaixo vemos inicialmente a força atuando sobre uma carga de prova positiva colocada no campo elétrico. A direção e o sentido da força elétrostática coincidem com a direção e o sentido do vetor campo.

Quando a carga de prova é negativa, a força tem a direção do vetor campo e sentido oposto ao dele.

Clique para ampliar

x

No sistema Internacional (SI) a intensidade da força é medida em newton (N), a carga elétrica em coulomb (C) e a intensidade do vetor campo em N/C.

Pense & Responda

Linhas de força

Borges e Nicolau
A cada ponto P de um campo elétrico associamos um único vetor campo elétrico. Com base neste fato, explique por que duas linhas de força nunca se cruzam.

Eletrostática

Clique para ampliar

Vetor Campo Elétrico

Borges e Nicolau
No campo elétrico de uma carga elétrica puntiforme fixa Q, o vetor campo elétrico num ponto P, situado a uma distância d da carga, tem intensidade E. A intensidade depende do meio onde a carga se encontra, é diretamente proporcional ao valor absoluto da carga e inversamente proporcional ao quadrado da distância do ponto à carga. Se Q for positiva o vetor campo elétrico é de afastamento. Se Q for negativa, o vetor campo elétrico é de aproximação. No caso do campo gerado por duas ou mais cargas elétricas puntiformes, cada uma originará, num ponto P, um vetor campo elétrico. O vetor campo resultante será obtido por meio da adição vetorial dos diversos vetores campos individuais no ponto P.

Pense & Responda

Clique para ampliar

Campo Elétrico

Borges e Nicolau
Vamos considerar o campo elétrico gerado por várias cargas elétricas puntiformes fixas. Qual é a intensidade do vetor campo elétrico resultante no ponto P do campo, nos casos indicados acima? Considere a carga Q positiva. Dê a resposta em função de E, intensidade do vetor campo elétrico no ponto P gerado por uma carga puntiforme Q individualmente.

Adição de vetores

Clique para ampliar

Caso (importante) particular

Borges e Nicolau
Em Física é comum a necessidade de se obter a soma de dois vetores - vetor resultante - de mesmo módulo e de direções formando ângulo de 120º.

No desenho acima temos na figura 1 dois vetores de módulo L.

Para obter o vetor resultante devemos colocar os segmentos orientados que representam os vetores, de forma consecutiva, como na figura 2.

O vetor resultante tem a direção da reta r que fecha o triângulo (figura 3). Sua origem coincide com a origem do segmento orientado que representa o primeiro vetor e, sua extremidade, com a extremidade do segundo (figura 4).

Da geometria concluimos que o módulo do vetor resultante é igual ao módulo dos vetores dados.

Portanto, somar dois vetores de mesmo módulo, formando ângulo de 120º, não deve tomar seu precioso tempo em uma prova. Não se esqueça.

Pense & Responda

Interação entre cargas elétricas

Borges e Nicolau
Cargas elétricas de mesmo sinal repelem-se. Cargas elétricas de sinais contrários atraem-se. A força de interação tem a direção da reta que une as cargas, depende do meio onde elas se encontram e é diretamente proporcional ao produto dos valores absolutos das cargas e inversamente proporcional ao quadrado da distância entre elas.

Na figura acima temos três cargas elétricas dispostas nos vertices A, B e C de um triângulo equilátero, todas de mesmo valor absoluto. As cargas em A e C são positivas e a carga em B é negativa.

Sabendo-se que a força de interação eletrostática entre as cargas situadas em A e C tem intensidade 10N, conforme indicado na figura, qual é a intensidade da força resultante na carga em C. E qual é a direção dessa força?

Mecânica

Composição de Movimentos

x

Borges e Nicolau

Um barco desloca-se nas águas de um rio. O movimento do barco em relação às águas é chamado movimento relativo. O movimento das águas em relação à Terra, isto é, em relação às margens é o movimento de arrastamento e o movimento do barco em relação à Terra (margem) é o movimento resultante. O estudo do movimento resultante a partir dos movimentos relativo e de arrastamento é denominado composição de movimento.

x

A velocidade do barco em relação às águas é a velocidade relativa (Vrel.). A velocidade das águas em relação à Terra é a velocidade de arrastamento (Varr.) e a velocidade do barco em relação à Terra é a velocidade resultante (Vres.). Estas velocidades relacionam-se pela igualdade vetorial:

Vamos analisar quatro situações de um barco movimentando-se num rio e relacionar os módulos da velocidade relativa, da velocidade de arrastamento e da velocidade resultante.

Clique para ampliar

Desafio de Mestre

Composição de movimentos

Borges e Nicolau
Considere um barco, movendo-se com velocidade de módulo v em relação à correnteza de um rio de margens paralelas. Seja μ<v o módulo da velocidade da correnteza em relação às margens. Vamos indicar por Δt1 e Δt2 os intervalos de tempo dos movimentos do barco em duas trajetórias:

(1) ABA: o barco vai de A até B (desce o rio) e retorna de B a A (sobe o rio).

(2) ACA : o barco atravessa a correnteza normalmente às margens, indo de A a C e retornando de C a A.

Os movimentos são uniformes e seja AB = AC = L.

Você sabe em que trajetória, ABA ou ACA, o barco é mais lento?

Leituras do Blog

Em busca do Éter

Borges e Nicolau
Até o final do século XIX, acreditava-se que o universo era preenchido por um meio elástico, onipresente e invisível, denominado éter, e que a luz e as ondas eletromagnéticas caminhavam com velocidade c em relação a esse meio. Como o éter era um meio hipotético, cuja existência jamais fora provada, os físicos estadunidenses Michelson e Morley realizaram, em Cleveland (1887), uma experiência para verificar sua existência.

Esses físicos consideraram que, se o espaço sideral estava preenchido por um mar de éter imóvel e que se a luz fosse realmente propagada através dele, sua velocidade deveria ser afetada pela corrente de éter resultante do movimento de translação da Terra. Como a Terra translada em relação ao Sol com velocidade aproximadamente igual a 30 km/s (valor conhecido na época da experiência de Michelson e Morley), de modo equivalente podemos supor a Terra estacionária e a corrente de éter movimentando-se com velocidade u ≈ 30 km/s no sentido oposto.

O movimento da corrente de éter seria o movimento de arrastamento. A propagação de um raio de luz, em relação ao éter, com velocidade
v = c ≈ 300.000 km/s, seria o movimento relativo.

Michelson e Morley construíram um aparelho denominado interferômetro, capaz de registra variações de até frações de km/s na enorme velocidade da luz.

No arranjo experimental, envia-se um raio de luz na direção da hipotética correnteza, descrevendo a trajetória ABA, análoga à do exercício Desafio do Mestre, enquanto que outro raio de luz descreve, normalmente à velocidade do éter, a trajetória ACA. Michelson e Morley mediram os intervalos de tempo Δt1 e Δt2 e esperavam encontrar o valor, Δt1/Δt2 = 1,00000001 correspondente à substituição, na equação abaixo, dos valores da velocidade da luz c ≈ 300.000 km/s e da velocidade de translação da Terra em sua órbita (u ≈ 30 km/s), equivalente à correnteza de éter.

Contudo realizada a experiência, a conclusão foi perturbadora: não havia nenhuma diferença entre os intervalos de tempo Δt1 e Δt2. Repetiu-se a experiência várias vezes, em épocas e condições técnicas diferentes, chegando-se ao mesmo resultado.

Duas conclusões podem ser tiradas da experiência de Michelson e Morley realizada para detectar algum efeito do éter no movimento dos raios de luz:

1) A velocidade da luz é constante e independente de qualquer movimento do éter.

2) Como decorrência da conclusão anterior, podemos abolir inteiramente a noção de éter.

Pense & Responda

As caixas do Seu Joaquim

Borges e Nicolau
Seu Joaquim deve levar três caixas idênticas, cada uma de peso P = 30N, para um depósito. Estas caixas estão dispostas conforme a figura A. Considere a existência de atrito entre as caixas e o piso horizontal. Seu Joaquim aplica à caixa 1 uma força horizontal de intensidade F e ela adquire uma aceleração a = 2 m/s².

A caixa 1 entra em contato com a caixa 2 e seu Joaquim continua aplicando ao sistema de caixas a mesma força (figura B), até encostar na caixa 3.

Sob ação da mesma força as três caixas em contato passam a escorregar em movimento retilíneo e uniforme, até chegar ao depósito (figura C).

Você saberia calcular a intensidade da força que seu Joaquim aplicou na caixa 1, a aceleração a’ adquirida pelas caixas 1 e 2 e a intensidade da força de atrito? Considere g = 10 m/s².

Alternativas energéticas

Energia Eólica

Nicolau Gilberto Ferraro e Sidney Borges
Energia eólica é uma das principais fontes alternativas de energia renovável. É produzida pelas correntes de ar que se formam na atmosfera. Estas correntes incidem sobre as pás da turbina, movimentando-as. Basicamente o gerador eólico funciona de maneira semelhante ao gerador de uma usina hidrelétrica.

A potência elétrica gerada é proporcional à densidade do ar, à área do círculo descrito pelas pás e ao cubo da velocidade com que o vento nelas incide.

São pontos positivos para a instalação de usinas eólicas:

 Utilização de energia natural.
 Redução significativa do custo do equipamento, nas duas últimas décadas.
 Baixo custo de produção de energia.
 Não contribui para o efeito estufa.
 Não há consumo de combustível.
 O vento é um recurso inesgotável

São pontos negativos:

 Alto investimento para a transmissão da energia elétrica gerada.
 Necessidade de condições adequadas de vento.
 Não é possível produzir energia elétrica sob demanda.
 Energia elétrica gerada por gerador eólico é relativamente pequena.
 Limitação de locais para instalação de geradores eólicos.
 Impacto ambiental: sonoro (ruído dos rotores) e visuais.
 Interferências nos sistemas de comunicação (rádio e TV)

Como funciona a energia eólica - parte 1

Como funciona a energia eólica - parte 2

Como funciona a energia eólica - parte 3

Energia Eólica

Pense & Responda

Energia Eólica

Muitos consideram que a energia eólica é uma fonte de energia que pode substituir as centrais térmicas movidas a petróleo ou a carvão. Os geradores eólicos apresentados na figura abaixo possuem pás que giram conforme o vento. Essas rotações fazem com que o gerador produza eletricidade.


Questão 1:

Os gráficos abaixo mostram a velocidade média do vento em quatro locais diferentes ao longo do ano. Qual o local mais apropriado para a instalação de um gerador eólico?

Clique para ampliar

Questão 2:

Quanto mais forte o vento, mais rapidamente giram as pás dos geradores eólicos e mais energia elétrica é gerada. No entanto, em uma situação real, não há uma relação direta entre a velocidade do vento e a energia elétrica produzida. Abaixo, apresentamos quatro condições de funcionamento de uma central de energia eólica em situação real.

x

1. As pás começarão a girar quando a velocidade do vento for v1.

2. Por razões de segurança, a rotação das pás não aumentará quando a velocidade do vento for maior que v2.

3. A potência elétrica está no máximo (W) quando o vento atinge a velocidade v2.

4. As pás irão parar de girar quando a velocidade do vento alcançar v3.

Qual dos gráficos a seguir melhor representa a relação entre a velocidade do vento e a energia elétrica gerada sob as condições de funcionamento descritas?

Clique para ampliar

x

Questão 3:

X

A uma mesma velocidade do vento, quanto mais elevada for a altitude, mais lenta será a rotação das pás. Qual das alternativas a seguir explica melhor por que as pás dos geradores eólicos giram mais lentamente em lugares mais altos, já que a velocidade do vento é a mesma?

x
A. O ar é menos denso, à medida que a altitude aumenta.
B. A temperatura é mais baixa, à medida que a altitude aumenta.
C. A gravidade torna-se menor, à medida que a altitude aumenta.
D. Chove com mais freqüência, quando a altitude aumenta.

X

Questão 4:

Descreva uma vantagem e uma desvantagem específicas da produção de energia eólica com relação à produção de energia a partir de combustíveis fósseis, como o carvão e o petróleo.

x
Vantagem_________________________________________________________ ______________________________________________________________

x

Desvantagem______________________________________________________ ______________________________________________________________

X

Nota: Questões do PISA. Programa Internacional de Avaliação de Alunos