Encontro no Rio de Janeiro
Borges e Nicolau
Na próxima semana, entre os dias 04 e 08 de outubro, acontecerá no Rio de Janeiro o VIII Encontro de Licenciatura em Física (ENLIF), promovido pelo Instituto de Física da UFRJ.
Para saber mais siga o link.
A necessidade do ser humano de compreender o ambiente que o cerca e explicar os fenômenos naturais é a gênese da Física.
Postagem em destaque
Como funciona o Blog
Aqui no blog você tem todas as aulas que precisa para estudar Física para a sua escola e para os vestibulares. As aulas são divididas em trê...
quinta-feira, 30 de setembro de 2010
Desafio de Mestre (Especial)
Análise dimensional
Borges e Nicolau
Considere a grandeza dada por:
onde G é a constante de Gravitação Universal, h a constante de Planck e c velocidade de propagação da luz no vácuo. Qual é a unidade da citada grandeza no Sistema Internacional?
Indicações para a resolução:
xxxxxLembre-se também que F = m.a
xxxxτ (τ = F.d)
Borges e Nicolau
Considere a grandeza dada por:
onde G é a constante de Gravitação Universal, h a constante de Planck e c velocidade de propagação da luz no vácuo. Qual é a unidade da citada grandeza no Sistema Internacional?
Indicações para a resolução:
- Escreva a unidade de G em função das unidades quilograma (kg), metro (m) e segundo (s). Para isso, utilize a Lei de Newton da Gravitação Universal:
xxxxxLembre-se também que F = m.a
- Escreva a unidade de h em função das unidades quilograma (kg), metro (m) e segundo (s). Para isso, utilize Equação de Planck E = h.f que fornece o quantum E de energia radiante de freqüência f.
xxxxτ (τ = F.d)
A Física do cotidiano
Eletrodinâmica
Respostas de 29/09
Borges e Nicolau
1) Raphael está montando um circuito elétrico em sua residência e necessita de 5 metros de fio de cobre, com a mais baixa resistência elétrica possível. O vendedor dispõe de três fios, de números 14, 12 e 10 e explica que quanto menor o número do fio maior é o diâmetro de sua seção reta. Qual dos fios Raphael escolheu?
Resposta:
Raphael escolheu o fio de número 10. Seu diâmetro é maior (fio mais grosso) e consequentemente sua resistência elétrica é menor. O material é o mesmo (cobre), assim como o comprimento do fio.
2) Celestino compra duas lâmpadas elétricas incandescentes de mesma potência, sendo uma para 127 V e outra para 220 V. Por engano liga a lâmpada para 127 V numa tomada de 220 V e a lâmpada para 220 V, numa tomada de 127 V. Na primeira situação a lâmpada queima. Pode-se afirmar que o mesmo acontece na segunda situação?
Resposta:
Não. A lâmpada para 220 V ligada numa tomada de 127 V não queima, mas apresenta brilho bem inferior ao de funcionamento normal.
3) As lâmpadas elétricas dos cômodos de uma casa são ligadas em paralelo, de modo que quando uma queima as outras apagam. A afirmação está certa ou errada?
Resposta:
A afirmação está errada, As lâmpadas dos diversos cômodos estão ligadas em paralelo, mas se uma queima as outra continuam funcionando normalmente.
4) Para a iluminação de uma escada utilizam-se duas chaves do tipo “paralela”, que possuem três terminais no lugar de dois. Uma chave fica no andar de baixo e a outra no andar de cima. Analise o circuito e explique como ele funciona.
Respostas de 29/09
Borges e Nicolau
1) Raphael está montando um circuito elétrico em sua residência e necessita de 5 metros de fio de cobre, com a mais baixa resistência elétrica possível. O vendedor dispõe de três fios, de números 14, 12 e 10 e explica que quanto menor o número do fio maior é o diâmetro de sua seção reta. Qual dos fios Raphael escolheu?
Resposta:
Raphael escolheu o fio de número 10. Seu diâmetro é maior (fio mais grosso) e consequentemente sua resistência elétrica é menor. O material é o mesmo (cobre), assim como o comprimento do fio.
2) Celestino compra duas lâmpadas elétricas incandescentes de mesma potência, sendo uma para 127 V e outra para 220 V. Por engano liga a lâmpada para 127 V numa tomada de 220 V e a lâmpada para 220 V, numa tomada de 127 V. Na primeira situação a lâmpada queima. Pode-se afirmar que o mesmo acontece na segunda situação?
Resposta:
Não. A lâmpada para 220 V ligada numa tomada de 127 V não queima, mas apresenta brilho bem inferior ao de funcionamento normal.
3) As lâmpadas elétricas dos cômodos de uma casa são ligadas em paralelo, de modo que quando uma queima as outras apagam. A afirmação está certa ou errada?
Resposta:
A afirmação está errada, As lâmpadas dos diversos cômodos estão ligadas em paralelo, mas se uma queima as outra continuam funcionando normalmente.
4) Para a iluminação de uma escada utilizam-se duas chaves do tipo “paralela”, que possuem três terminais no lugar de dois. Uma chave fica no andar de baixo e a outra no andar de cima. Analise o circuito e explique como ele funciona.
Clique para ampliar
Resposta:
Cada uma das chaves permite acender ou apagar a lâmpada que ilumina a escada, independentemente da posição da outra chave. Assim, com a chave C1 na posição 2 a lâmpada está acessa. Passando para a posição 1, apagamos a lâmpada. O mesmo podemos fazer com a chave C2 do andar de cima. Se a chave C2 estiver na posição 4 e a chave C1 na posição 2, a lâmpada estará acesa. Se a chave for colocada na posição 3 a lâmpada será apagada.
5) O ebulidor elétrico é um equipamento constituído essencialmente por um resistor, em forma de hélice e destina- se a aquecer ou levar à fervura um determinado líquido, como por exemplo a água. Um ebulidor foi ligado, sem estar imerso na água e seu resistor queimou rapidamente. Explique por que isso ocorreu.
Resposta:
Não estando mergulhado na água, ocorre menor transferência de calor para o meio ambiente. Deste modo, a temperatura do resistor vai aumentando até sua fusão.
Pense & Responda
Içamento de uma carga perigosa
Clique para ampliar
Borges e Nicolau
O esquema mostra uma carga situada no fundo do mar. Para içá-la utiliza-se um balão no qual foi injetado um gás. Na figura representamos o instante em que a carga está em equilíbrio, mas prestes a subir. Sendo a massa do balão igual a 102 kg e 1 m3 seu volume, determine no instante considerado a intensidade da força de tração no cabo, sabendo-se que a densidade da água é igual a 103 kg/m3 e g = 10 m/s2.
quarta-feira, 29 de setembro de 2010
A Física do cotidiano
Eletrodinâmica
Borges e Nicolau
1) Raphael está montando um circuito elétrico em sua residência e necessita de 5 metros de fio de cobre com a mais baixa resistência elétrica possível. O vendedor dispõe de três fios, de números 14, 12 e 10 e explica que quanto menor o número do fio maior é o diâmetro de sua seção reta. Qual dos fios Raphael escolheu?
2) Celestino compra duas lâmpadas elétricas incandescentes de mesma potência, sendo uma para 127 V e outra para 220 V. Por engano liga a lâmpada para 127 V numa tomada de 220 V e a lâmpada para 220 V numa tomada de 127 V. Na primeira situação a lâmpada queima. Pode-se afirmar que o mesmo acontece na segunda situação?
3) As lâmpadas elétricas dos cômodos de uma casa são ligadas em paralelo, de modo que quando uma queima as outras apagam. A afirmação está certa ou errada?
4) Para a iluminação de uma escada utilizam-se duas chaves do tipo “paralela”, que possuem três terminais no lugar de dois. Uma chave fica no andar de baixo e a outra no andar de cima. A chave C1 pode ocupar as posições 1 ou 2 e a chave C2 as posições 3 ou 4. Analise o circuito e explique como ele funciona.
5) O ebulidor elétrico é um equipamento constituído essencialmente por um resistor em forma de hélice e destina-se a aquecer ou levar à fervura um determinado líquido, como por exemplo a água. Um ebulidor foi ligado sem estar imerso na água e seu resistor queimou rapidamente. Explique por que isso ocorreu.
Borges e Nicolau
1) Raphael está montando um circuito elétrico em sua residência e necessita de 5 metros de fio de cobre com a mais baixa resistência elétrica possível. O vendedor dispõe de três fios, de números 14, 12 e 10 e explica que quanto menor o número do fio maior é o diâmetro de sua seção reta. Qual dos fios Raphael escolheu?
2) Celestino compra duas lâmpadas elétricas incandescentes de mesma potência, sendo uma para 127 V e outra para 220 V. Por engano liga a lâmpada para 127 V numa tomada de 220 V e a lâmpada para 220 V numa tomada de 127 V. Na primeira situação a lâmpada queima. Pode-se afirmar que o mesmo acontece na segunda situação?
3) As lâmpadas elétricas dos cômodos de uma casa são ligadas em paralelo, de modo que quando uma queima as outras apagam. A afirmação está certa ou errada?
4) Para a iluminação de uma escada utilizam-se duas chaves do tipo “paralela”, que possuem três terminais no lugar de dois. Uma chave fica no andar de baixo e a outra no andar de cima. A chave C1 pode ocupar as posições 1 ou 2 e a chave C2 as posições 3 ou 4. Analise o circuito e explique como ele funciona.
Clique para ampliar
5) O ebulidor elétrico é um equipamento constituído essencialmente por um resistor em forma de hélice e destina-se a aquecer ou levar à fervura um determinado líquido, como por exemplo a água. Um ebulidor foi ligado sem estar imerso na água e seu resistor queimou rapidamente. Explique por que isso ocorreu.
terça-feira, 28 de setembro de 2010
Pense & Responda
Clique para ampliar
O arquiteto de Cleópatra
Borges e Nicolau
O arquiteto preferido de Cleópatra, Phideas III, desenhou o aprazível recanto que mostramos acima. Cada uma das três lajes apoiadas na coluna de capitel retilíneo, última moda no Mediterrâneo, tem massa igual a 12 toneladas (1 tonelada = 1000 kg). As lajes estão solidarizadas com uma cola especial inventada na Gália. Para equilibrar o conjunto o grande artista ficou em dúvida. Qual deve ser a massa da esfera A para que haja equilibrio e Cleópatra possa desfrutar de momentos reflexivos em sua moderníssima "chaise longue", sem que o céu, ou melhor, o teto desabe sobre sua cabeça? Despreze as dimensões do apoio.
Desafio de Mestre (Especial)
Clique para ampliar
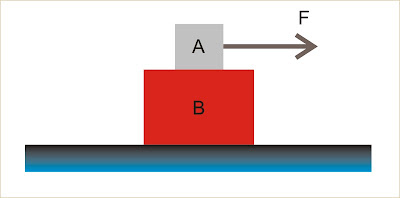
Sem escorregar
Borges e Nicolau
Qual é a intensidade da força horizontal F que deve ser constantemente aplicada no bloco A, de massa M = 5,0 kg , para que o bloco B, de massa
m = 1,0 kg , permaneça em repouso em relação ao bloco A? Não existe atrito entre o bloco A e o solo horizontal e nem entre A e B.
Dados: sen θ = 0,60, cos θ = 0,80 e g = 10m/s2.
Orientação para a resolução:
• Aplique o princípio fundamental da Dinâmica para o bloco B e calcule a aceleração do sistema de blocos.
• Aplique o princípio fundamental da Dinâmica para o conjunto (A+B) e calcule F.
segunda-feira, 27 de setembro de 2010
Preparando-se para as Provas
Trabalho e Energia
Borges e Nicolau
Exercício 1
Seu Joaquim arrasta uma caixa ao longo de um plano inclinado, visando colocá-la na carroceria de um caminhão.
Exercício 4
Borges e Nicolau
Exercício 1
Seu Joaquim arrasta uma caixa ao longo de um plano inclinado, visando colocá-la na carroceria de um caminhão.
Clique para ampliar
Ele aplica na caixa uma força paralela ao plano inclinado e cuja intensidade F varia com a distância, conforme indica o gráfico abaixo.
Clique para ampliar
São dadas as intensidades das outras forças que agem na caixa:
• Peso: P = 60 N
• Força de atrito: Fat = 7,0 N
• Força normal: FN = 58 N
Calcule o trabalho realizado pelas forças que agem na caixa no deslocamento do solo (C) até a carroceria do caminhão (A).
Sabe-se que AB = 1,5 m e AC = 6,0 m
Exercício 2
Retome o exercício anterior. Se a caixa saiu do repouso de C, com que velocidade atingiu a carroceria em A? Considere g = 10 m/s2
Exercício 3
Uma bolinha é lançada verticalmente, a partir do solo (ponto A), com energia cinética de 30 J. Adote o solo como nível de referência para a medida da energia potencial gravitacional. Seja h a altura máxima atingida pela bolinha (ponto B). Os pontos C e D da trajetória estão situados, respectivamente, a h/3 e 2h/3 do solo. Despreze os atritos. Preencha a tabela:
Clique para ampliar
Exercício 4
Uma pequena esfera é abandonada do ponto A e efetua um looping. Calcule a velocidade da esfera ao passar pelas posições B e C, indicadas na figura. Despreze os atritos e considere dados o raio R da trajetória circular e a aceleração local da gravidade g.
Clique para ampliar
Exercício 5
Um menino desce por um escorregador de altura 4,0 m, a partir do repouso. Considerando g = 10 m/s2 e que 20% da energia mecânica é dissipada durante o trajeto, determine a velocidade com que o menino atinge o solo.
Clique para ampliar
domingo, 26 de setembro de 2010
Arte do Blog
Clique para ampliar
Noite Estrelada sobre o Rhone
Borges e Nicolau
Na obra acima a beleza esfuziante do céu noturno foi integralmente capturada pelos pincéis e tintas de Vincent van Gogh, artista dotado de imenso talento que viveu na segunda metade do século XIX. Dificilmente uma fotografia faria melhor representação. Durante sua breve vida (1853-1890) o inquieto Vincent contemplou as estrelas e as reproduziu em telas coloridas.
A representação do firmamento foi um desafio contínuo, sempre presente em sua obra. No quadro "Noite Estrelada sobre o Rhone" a cidade francesa de Arles aparece retratada com as luzes dos lampiões de gás refletindo no rio Ródano (em Francês Rhone). O céu noturno resplandece em brilho, vivo, com imagens das estrelas explodindo em luminosidade e fazendo contraponto com os tons fortes do fundo azul profundamente escuro. Acima do rio, pode-se discernir as estrelas da constelação Ursa Maior.
Saiba mais sobre a Ursa Maior aqui
Resolução do Desafio de Mestre Especial - 21/09
Clique para ampliar
Deslizando com atrito
Borges e Nicolau
Os blocos A e B, representados na figura, possuem massas 2,0 kg e 8,0 kg, respectivamente. Uma força horizontal F é aplicada ao bloco B. O coeficiente de atrito dinâmico entre A e B e entre B e o solo é igual a 0,30. Os blocos A e B deslocam-se em movimento retilíneo uniforme. Considere o fio e a polia ideais e g = 10 m/s2.
a) Represente as forças que agem em A e B.
b) Determine a intensidade da força F e a intensidade da força de tração no fio.
Resolução:
a) Representação das forças que agem em A e B
Clique para ampliar
b) Como os blocos realizam MRU a resultante das forças que agem neles é nula. Assim, temos:
Bloco A:
FNA = P = > FNA = 20 N
T = FatBA = > T = μ.FNA = > T = 0,30 . 20 = > T = 6,0 N
Bloco B:
FNB = FNA + PB = > FNB = 20 + 80 = > FNB = 100 N
F = T + FatAB + Fat = > F = T + FatAB + μ.FNB = >
F = 6,0 + 6,0 + 0,30.100 = >
F = 42 N
sábado, 25 de setembro de 2010
Leituras do Blog

As forças fundamentais da Natureza
Borges e Nicolau
A força de interação entre partículas dotadas de massa é a força gravitacional. A força gravitacional explica a movimentação dos astros no Universo, bem como a formação de estrelas, galáxias e sistemas planetários.
A força eletromagnética é a que se manifesta entre partículas eletrizadas, englobando as forças elétricas e as forças magnéticas. A força eletromagnética é que mantêm os elétrons ligados aos núcleos dos átomos. O núcleo é constituído de prótons (dotados de carga elétrica positiva) e de nêutrons. Entre os prótons do núcleo têm-se força de repulsão que é uma força eletromagnética. Mas se os prótons se repelem por que não ocorre a desintegração do núcleo? É a força nuclear forte que mantém coesão do núcleo atômico, garantindo a união dos quarks para formarem os prótons e os nêutrons, assim como a ligação dos prótons entre si e dos prótons com os nêutrons. As forças nucleares têm alcance muito curto, da ordem das dimensões dos núcleos atômicos. São as mais intensas das forças fundamentais da natureza. A força responsável pela emissão de elétrons por parte dos núcleos de algumas substâncias radioativas, num processo denominado decaimento beta, é a força nuclear fraca. Atualmente, a maior parte dos cientistas admite que as forças nuclear fraca e eletromagnética são manifestações diferentes de uma mesma interação fundamental, chamando-as de força eletrofraca.
Pense & Responda
Das quatro forças fundamentais da natureza, como você classificaria a força de atrito? E a força de tração num fio e o peso de um corpo?
Os quarks
Os prótons e nêutrons são constituídos de partículas chamadas quarks. Existem três duplas de quarks: up e down; charm e strange; top e botton. As cargas elétricas dos quarks up e down são, respectivamente, +2e/3 e - e/3, onde e é a carga elétrica elementar. O próton é constituído de dois quarks up e um quark down. O nêutron é formado por dois quarks down e um quark up.
Resolução de "Preparando-se para as provas"
Leis de Newton e Atrito
Clique para ampliar
Exercício 1
Seu Joaquim empurra uma caixa que escorrega ao longo do solo horizontal. Ao atingir a velocidade v = 3,0 m/s, seu Joaquim deixa de empurrar a caixa que se desloca 1,5 m até parar. Adote g = 10 m/s2. Qual é o coeficiente de atrito dinâmico entre a caixa e o solo?
Resolução
Clique para ampliar
Pela equação de Torricelli:
vf2 = v2 + 2αΔS = > 0 = 3,02 + 2α.1,5 = > α = -3,0 m/s2
Pelo Princípio Fundamental da Dinâmica:
Fat = m.a = > μ.FN = m.a = > = > μ.mg = ma = > a = μ.g
Sendo a = IαI = 3,0 m/s2 e g = 10 m/s2, vem: μ = 0,30
Clique para ampliar
Exercício 2
Aplica-se numa caixa, de peso P = 44 N, uma força de intensidade
F= 20 N, conforme indica a figura. Sendo sen θ = 0,60 e cos θ = 0,80 e considerando-se a caixa na iminência de escorregar, determine o coeficiente de atrito estático entre a caixa e o solo.
Resolução:
Clique para ampliar
No equilíbrio, temos:
F sen θ + FN = P = > 20 . 0,60 + FN = 44 = > FN = 32 N
F cos θ = Fat = > F cos θ = μ . FN = > 20 . 0,80 = μ . 32 = >
μ = 0,50
Clique para ampliar
Exercício 3
a) Calcule a aceleração dos blocos A e B, de mesma massa m, considerando que não existe atrito entre o bloco B e o plano inclinado.
b) Sendo os coeficientes de atrito estático e dinâmico entre B e o plano inclinado iguais a 0,20, verifique se o sistema abandonado em repouso entra em movimento. Em caso afirmativo, calcule a aceleração dos blocos.
São dados: sen θ = 0,60, cos θ = 0,80 e g = 10m/s2
Considere o fio e a polia ideais.
Resolução:
Clique para ampliar
a) Pelo Princípio Fundamental da Dinâmica:
Bloco A: m.g - T = m.a (1)
Bloco B: T - mg. sen θ = m.a (2)(1) + (2):
m.g - m.g.sen θ = 2 m.a = > a = g.(1 - sen θ)/2 = >
a = 10.(1 - 0,60)/2
a = 2,0 m/s2
Clique para ampliar
b) Inicialmente observe que o sistema entra em movimento pois o peso do bloco A (m.g) é maior do que Fat + Pt.
De fato: Fat + Pt = μ.m.g. cos θ + m.g. sen θ = 0,20.m.g.0,80 + mg.0,60 = 0,76.m.g
Pelo Princípio Fundamental da Dinâmica:
Bloco A: m.g - T = m.a (1)
Bloco B: T - Fat - Pt = m.a (2)
(1) + (2):
m.g - (Fat + Pt) = 2.m.a = > m.g - 0,76.m.g = 2m.a
a = 1,2 m/s2
Clique para ampliar
Exercício 4
Na figura, A e B são dois blocos de massas 4,0 kg e 6,0 kg, respectivamente. Não há atrito entre B e o solo horizontal. Uma força horizontal de intensidade F = 30 N é aplicada no bloco B, de modo que não ocorre escorregamento de um bloco em relação ao outro.
Determine a aceleração dos blocos e a intensidade da fora de atrito que B exerce em A.
Resolução:
Pelo princípio fundamental da Dinâmica aplicado ao conjunto (A+B):
F = (mA + mB).a = > 30 = 10.a = > = 3,0 m/s2
A força que acelera A é a força de atrito que B exerce em A:
Clique para ampliar
Assim: Fat = mA.a = Fat = 12 N
Clique para ampliar
Refaça o exercício anterior. Quais seriam as respostas se a força F fosse aplicada no bloco A? Considere que um bloco não escorregue em relação ao outro.
Resolução:
Pelo princípio fundamental da Dinâmica aplicado ao conjunto (A+B):
F = (mA + mB).a = > 30 = 10.a = > = 3,0 m/s2Considerando o bloco A, vem:
F - Fat = mA.a = > 30 - Fat = 4,0 . 3,0 = > Fat = 18 N
Clique para ampliar
Resolução de Ordem de Grandeza
Avalie, Calcule & Responda
Borges e Nicolau
Questão 1
Pedro fez uma caminhada no parque de sua cidade. Ele queria saber a distância percorrida durante uma volta. Para isso, observou que dava 100 passos normais durante um minuto. Se o tempo total para completar a volta foi de ¾ de hora, pode-se afirmar que a volta:
a) é maior do que 5 km
b) está entre 2,5 km e 3,5 km
c) está entre 1,5 km e 2 km
d) é menor do que 1 km
Resolução:
Considerando o comprimento de um passo normal de 75 cm, concluímos que ao completar 100 passos Pedro percorre 7500 cm = 75 m, em um minuto. Como ¾ de hora corresponde a 45 minutos, podemos avaliar extensão de uma volta: 75 (metros por minuto) X 45 (minutos) = 3375 m ≈ 3,4 km
RESPOSTA: B
Questão 2
Júlia faz hoje 15 anos. Ela calculou o número de vezes que seu coração bateu desde seu nascimento. Encontrou um valor:
a) igual a 120 mil batimentos
b) entre 1 milhão e 2 milhões de batimentos
c) 5 milhões de batimentos
d) maior do que 300 milhões de batimentos
Resolução:
Vamos considerar que o coração bata 70 vezes por minuto. Calculemos o número de minutos existentes em 15 anos:
15 anos = 15x365x24x60 minutos = 7 884 000 minutos.
Número de batimentos em 15 anos de vida:
7 884 000 (minutos) x 70 (batimentos por minuto) = 551 880 000 batimentos ≈ 550 milhões de batimentos
RESPOSTA: D
Questão 3
Numa viagem de 100 km, qual é o número de voltas dadas pela roda de um automóvel?
a) 2 mil voltas
b) 5 mil voltas
c) entre 5 mil e 15 mil voltas
d) mais do que 30 mil voltas.
Resolução:
Considerando o raio da roda igual a 30 cm, temos o seguinte número de voltas ao percorrer 100 km:
100 000 (metros) / 2π.0,30 (metros) = 53 000 voltas
RESPOSTA: D
Questão 4
O clube que Eneida freqüenta tem uma piscina de 5 m de largura por 10 m de comprimento e 1m de profundidade. Eneida resolveu calcular o número de gotas de água necessária para encher a piscina. Fazendo uma pesquisa ela descobriu que em um volume de 1 cm3 cabem 20 gotas de água. Qual é o número de gotas de água contidas na piscina?
a) 10 mil gotas
b) 100 mil gotas
c) 1 milhão de gotas
d) 1 bilhão de gotas
Resolução:
Vamos calcular o volume da piscina:
5 m x 10 m x 1m = 50 m3 = 50.106 cm3
Número de gotas de água contidas na piscina:
50.106 (cm3) x 20 gotas/cm3 = 1 bilhão de gotas
RESPOSTA: D
Borges e Nicolau
Questão 1
Pedro fez uma caminhada no parque de sua cidade. Ele queria saber a distância percorrida durante uma volta. Para isso, observou que dava 100 passos normais durante um minuto. Se o tempo total para completar a volta foi de ¾ de hora, pode-se afirmar que a volta:
a) é maior do que 5 km
b) está entre 2,5 km e 3,5 km
c) está entre 1,5 km e 2 km
d) é menor do que 1 km
Resolução:
Considerando o comprimento de um passo normal de 75 cm, concluímos que ao completar 100 passos Pedro percorre 7500 cm = 75 m, em um minuto. Como ¾ de hora corresponde a 45 minutos, podemos avaliar extensão de uma volta: 75 (metros por minuto) X 45 (minutos) = 3375 m ≈ 3,4 km
RESPOSTA: B
Questão 2
Júlia faz hoje 15 anos. Ela calculou o número de vezes que seu coração bateu desde seu nascimento. Encontrou um valor:
a) igual a 120 mil batimentos
b) entre 1 milhão e 2 milhões de batimentos
c) 5 milhões de batimentos
d) maior do que 300 milhões de batimentos
Resolução:
Vamos considerar que o coração bata 70 vezes por minuto. Calculemos o número de minutos existentes em 15 anos:
15 anos = 15x365x24x60 minutos = 7 884 000 minutos.
Número de batimentos em 15 anos de vida:
7 884 000 (minutos) x 70 (batimentos por minuto) = 551 880 000 batimentos ≈ 550 milhões de batimentos
RESPOSTA: D
Questão 3
Numa viagem de 100 km, qual é o número de voltas dadas pela roda de um automóvel?
a) 2 mil voltas
b) 5 mil voltas
c) entre 5 mil e 15 mil voltas
d) mais do que 30 mil voltas.
Resolução:
Considerando o raio da roda igual a 30 cm, temos o seguinte número de voltas ao percorrer 100 km:
100 000 (metros) / 2π.0,30 (metros) = 53 000 voltas
RESPOSTA: D
Questão 4
O clube que Eneida freqüenta tem uma piscina de 5 m de largura por 10 m de comprimento e 1m de profundidade. Eneida resolveu calcular o número de gotas de água necessária para encher a piscina. Fazendo uma pesquisa ela descobriu que em um volume de 1 cm3 cabem 20 gotas de água. Qual é o número de gotas de água contidas na piscina?
a) 10 mil gotas
b) 100 mil gotas
c) 1 milhão de gotas
d) 1 bilhão de gotas
Resolução:
Vamos calcular o volume da piscina:
5 m x 10 m x 1m = 50 m3 = 50.106 cm3
Número de gotas de água contidas na piscina:
50.106 (cm3) x 20 gotas/cm3 = 1 bilhão de gotas
RESPOSTA: D
Resolução de Empilhando livros
Clique para ampliar
No limiar da queda!
Borges e Nicolau
Você deseja empilhar os três livros da coleção “Os Fundamentos da Física”, conforme mostra a figura. Para que o conjunto fique em equilíbrio, quais os valores máximos das distâncias x e y indicadas? Considere os livros idênticos e que o centro de gravidade de cada um coincida com seu centro geométrico. É dada a largura L de cada livro.Clique para ampliar
sexta-feira, 24 de setembro de 2010
Leituras do Blog
Força de coesão e força de adesão
Borges e Nicolau
Ao analisarmos o fenômeno da tensão superficial, falamos em força de coesão que é a força de atração entre moléculas de uma mesma substância. A força de atração entre moléculas de diferentes substâncias é chamada força de adesão.
Capilaridade
Um tubo de pequeno diâmetro (tubo capilar) e aberto nas extremidades é colocado verticalmente num recipiente contendo um líquido. Duas situações podem ser observadas:
1ª) O líquido sobe no tubo capilar (ascensão de capilaridade)
2ª) O líquido desce no tubo capilar (depressão de capilaridade).
A primeira situação ocorre, por exemplo, no caso em que o líquido é a água e o tubo capilar é de vidro. É explicada pelo fato de a força de adesão entre as moléculas do vidro e da água ser maior do que a força de coesão entre as moléculas de água. Assim, a água adere ao tubo de vidro (a água molha o vidro), formando pequena película de curvatura côncava. Esta película, em virtude da tensão superficial, suporta a parte de água do tubo que fica acima do nível existente no recipiente.
Quanto mais fino for o tubo mais acentuado é o efeito.
A segunda situação ocorre, por exemplo, no caso em que o líquido é o mercúrio e o tubo capilar é de vidro. É explicada pelo fato de a força de adesão entre as moléculas do vidro e da água ser menor do que a força de coesão entre as moléculas de água. Assim, o mercúrio não adere ao tubo de vidro (o mercúrio não molha o vidro), formando pequena película de curvatura convexa. Esta película, em virtude da tensão superficial, é responsável pelo fato de o líquido descer no tubo.
A capilaridade explica muitos fenômenos que observamos cotidianamente. Por exemplo, a seiva bruta desloca-se pelos microscópicos vasos lenhosos das plantas, desde as raízes até as folhas, por capilaridade. Por esse processo a água atinge o topo das árvores, mesmo sendo muito altas, como as sequóias.
Também é possivel observar o fenômeno da capilaridade colocando o caule de uma flor branca dentro de um recipiente com água na qual foi dissolvido um corante. As pétalas da flor ficam coloridas por capilaridade.
Se você colocar a ponta de um guardanapo de papel num recipiente com água, constatará que a água sobe pelos espaços existentes no guardanapo que funcionam como tubos capilares.
Para ver mais detalhes e novas experiências:
Clique aqui e aqui e aqui
Borges e Nicolau
Ao analisarmos o fenômeno da tensão superficial, falamos em força de coesão que é a força de atração entre moléculas de uma mesma substância. A força de atração entre moléculas de diferentes substâncias é chamada força de adesão.
Capilaridade
Um tubo de pequeno diâmetro (tubo capilar) e aberto nas extremidades é colocado verticalmente num recipiente contendo um líquido. Duas situações podem ser observadas:
1ª) O líquido sobe no tubo capilar (ascensão de capilaridade)
2ª) O líquido desce no tubo capilar (depressão de capilaridade).
Clique para ampliar
A propriedade que um líquido possui de subir ou descer num tubo de pequeno diâmetro é denominada capilaridade.
Quanto mais fino for o tubo mais acentuado é o efeito.
A segunda situação ocorre, por exemplo, no caso em que o líquido é o mercúrio e o tubo capilar é de vidro. É explicada pelo fato de a força de adesão entre as moléculas do vidro e da água ser menor do que a força de coesão entre as moléculas de água. Assim, o mercúrio não adere ao tubo de vidro (o mercúrio não molha o vidro), formando pequena película de curvatura convexa. Esta película, em virtude da tensão superficial, é responsável pelo fato de o líquido descer no tubo.
A capilaridade explica muitos fenômenos que observamos cotidianamente. Por exemplo, a seiva bruta desloca-se pelos microscópicos vasos lenhosos das plantas, desde as raízes até as folhas, por capilaridade. Por esse processo a água atinge o topo das árvores, mesmo sendo muito altas, como as sequóias.
Sequoia sempervirens. Saiba mais aqui
Também é possivel observar o fenômeno da capilaridade colocando o caule de uma flor branca dentro de um recipiente com água na qual foi dissolvido um corante. As pétalas da flor ficam coloridas por capilaridade.
Se você colocar a ponta de um guardanapo de papel num recipiente com água, constatará que a água sobe pelos espaços existentes no guardanapo que funcionam como tubos capilares.
Para ver mais detalhes e novas experiências:
Clique aqui e aqui e aqui
quinta-feira, 23 de setembro de 2010
Leituras do Blog
Tensão superficial
Borges e Nicolau
Ao colocarmos uma pequena colher de aço num recipiente com água ela afunda, pois a densidade do aço é maior do que a da água. Mas por que ao colocarmos horizontalmente, com cuidado, uma agulha de aço sobre a superfície da água, ela não afunda? A resposta é que a superfície da água comporta-se como uma membrana elástica em tensão que resiste a se romper.
Borges e Nicolau
Ao colocarmos uma pequena colher de aço num recipiente com água ela afunda, pois a densidade do aço é maior do que a da água. Mas por que ao colocarmos horizontalmente, com cuidado, uma agulha de aço sobre a superfície da água, ela não afunda? A resposta é que a superfície da água comporta-se como uma membrana elástica em tensão que resiste a se romper.
Este fenômeno é denominado tensão superficial e ocorre não só com a água, mas também com outros líquidos. A formação desta membrana explica por que a água fica acima da borda de um copo, sem derramar, quando está na iminência de transbordar.

Como se explica a formação desta membrana? Considere uma molécula A de água no interior e outra B, na superfície. A molécula interna A está em equilíbrio sob ação das forças de coesão exercidas pelas moléculas que a rodeiam. Já a molécula B está sujeita a forças de coesão por partes das moléculas superficiais e daquelas que estão abaixo. A resultante das forças de coesão que age em B esta orientada para baixo. Assim, a camada superficial funciona como uma membrana, comprimindo as moléculas de baixo.


Clique para ampliar
Devido a este fenômeno a área superficial de um líquido tende a tornar-se a menor possível. Por isso, na ausência de forças externas as gotas de um líquido tendem a assumir a forma esférica que é a de menor área para um dado volume. No interior das naves espaciais, devido a imponderabilidade, as gotas de qualquer líquido solto no ambiente, assumem a forma esférica.
Clique aqui e aqui
Os detergentes diminuem a tensão superficial da água, permitindo que ela penetre com maior facilidade em locais de difícil acesso como cantos e orifícios pequenos, o que auxilia na limpeza de utensílios. Uma agulha colocada na superfície da água e suportada pela tensão superficial afunda quando algumas gotas de detergente são despejadas no recipiente.
Clique aqui e aqui
Assinar:
Postagens (Atom)