Lei de Coulomb (I)
Borges e Nicolau
Lei de Coulomb
A intensidade da força de ação mútua entre duas cargas elétricas puntiformes é diretamente proporcional ao produto dos valores absolutos das cargas e inversamente proporcional ao quadrado da distância que as separa.
k: constante eletrostática do meio onde estão as cargas.
No vácuo:
Animação:
Gráfico - Força x distância
Clique aqui
Interaja com a animação: clique na esfera 2 afaste e aproxime da esfera 1.
Exercícios básicos
Exercício 1:
Duas partículas igualmente eletrizadas estão separadas pela distância de 20 cm. A força eletrostática com que elas interagem tem intensidade de 3,6 N. O meio é o vácuo (k0 = 9.109 N.m2/C2).
a) Entre as partículas ocorre atração ou repulsão?
b) Qual é o valor da carga elétrica de cada partícula?
c) Sendo 1,6.10-19 C a carga elétrica elementar (carga elétrica do próton que em módulo é igual à carga elétrica do elétron), qual é o número de elétrons (em excesso ou em falta) que constitui a carga elétrica de cada partícula?
Resolução: clique aqui
Exercício 2:
Duas partículas eletrizadas com cargas elétricas Q1 e Q2, separadas pela distância d, atraem-se com uma força eletrostática de intensidade F. O meio é o vácuo. Determine em função de F a intensidade da força eletrostática de interação entre as partículas, nos casos:
a) Mantêm-se os valores de Q1 e Q2 e dobra-se a distância entre as partículas.
b) Mantêm-se os valores de Q1 e Q2 e triplica-se a distância entre as partículas.
c) Mantém-se a distância d e duplicam-se os valores das cargas elétricas das partículas.
d) Duplicam-se os valores das cargas elétricas das partículas e a distância d entre elas.
Resolução: clique aqui
x
Exercício 3:
Considere três partículas igualmente eletrizadas, cada uma com carga elétrica Q e fixas nos pontos A, B e C. Entre A e B a força eletrostática de repulsão tem intensidade 8,0.10-2 N. Qual é a intensidade da força eletrostática resultante das ações de A e C sobre B?
Resolução: clique aqui
Exercício 4:
Duas pequenas esferas metálicas idênticas estão eletrizadas com cargas elétricas +Q e –3Q. Situadas a uma distância d, as esferas atraem-se com uma força eletrostática de intensidade F = 9,0.10-2 N. As esferas são colocadas em contato e depois de alguns instantes são recolocadas em suas posições originais. Qual é a nova intensidade da força de interação eletrostática entre as esferas. Esta nova força é de atração ou de repulsão?
Resolução: clique aqui
Exercício 5:
Uma pequena esfera A, eletrizada com carga elétrica Q = 10-8 C, está fixa num ponto O. Outra pequena esfera eletrizada, B, com mesma carga elétrica e de massa 1 mg (miligrama) é colocada na vertical que passa pelo ponto O e acima deste ponto. Observa-se que B fica em equilíbrio. Determine a distância entre A e B.
Dados: k0 = 9.109 N.m2/C2; g = 10 m/s2
Resolução: clique aqui
A necessidade do ser humano de compreender o ambiente que o cerca e explicar os fenômenos naturais é a gênese da Física.
Postagem em destaque
Como funciona o Blog
Aqui no blog você tem todas as aulas que precisa para estudar Física para a sua escola e para os vestibulares. As aulas são divididas em trê...
quarta-feira, 29 de fevereiro de 2012
terça-feira, 28 de fevereiro de 2012
Cursos do Blog - Termologia, Óptica e Ondas
Dilatação térmica
Borges e Nicolau
A dilatação térmica é o aumento da distância entre as partículas de um sistema causado pelo aumento da temperatura. Do ponto de vista macroscópico, esse fenômeno é percebido como aumento das dimensões do sistema.
Dilatação térmica dos sólidos
Dilatação linear
Verifica-se experimentalmente que ΔL é proporcional a L0 e a Δθ:
em que α é o coeficiente de dilatação linear.
Sendo ΔL = L - L0, vem:
Dilatação superficial
Analogamente temos:
em que β é o coeficiente de dilatação superficial.
Relação:
Dilatação volumétrica
Analogamente temos:
em que γ é o coeficiente de dilatação volumétrica.
Relação:
Exercícios básicos
Exercício 1:
Uma lâmina bimetálica é constituída por duas tiras justapostas feitas de metais diferentes. Um dos metais (vamos chamá-lo de A) possui coeficiente de dilatação maior do que o outro (que chamaremos de B). Na temperatura ambiente a lâmina está reta. Ao ser aquecida a lâmina sofre um encurvamento. Nestas condições, o metal A constitui o arco externo ou interno da lâmina?
Resolução: clique aqui
Exercício 2:
Por que nas ferrovias os trilhos são assentados com um espaço entre eles?
Resolução: clique aqui
Exercício 3:
Numa aula de dilatação térmica o professor colocou a seguinte questão: aquece-se uma placa metálica com um furo no meio. O que ocorre com a placa e o furo? Para que os alunos discutissem o professor apresentou três possibilidades:
a) a placa e o furo dilatam.
b) a placa dilata e o furo contrai.
c) a placa contrai e o furo dilata.
Qual você escolheria como correta?
Resolução: clique aqui
Exercício 4:
Uma barra metálica de comprimento 2,0.102 cm, quando aquecida de
25 ºC a 50 ºC sofre um aumento em seu comprimento de 1,0.10-2 cm. Qual é o coeficiente de dilatação linear do material que constitui a barra?
Resolução: clique aqui
Exercício 5:
O coeficiente de dilatação superficial do alumínio é igual a 44.10-6 ºC-1. Determine o coeficiente de dilatação volumétrica do alumínio.
Resolução: clique aqui
Exercício 6:
Um bloco metálico é aquecido de 20 ºC a 120 ºC e seu volume sofre um acréscimo de 3%. Qual é o coeficiente de dilatação linear do material que constitui o bloco?
Resolução: clique aqui
Borges e Nicolau
A dilatação térmica é o aumento da distância entre as partículas de um sistema causado pelo aumento da temperatura. Do ponto de vista macroscópico, esse fenômeno é percebido como aumento das dimensões do sistema.
Dilatação térmica dos sólidos
Dilatação linear
Verifica-se experimentalmente que ΔL é proporcional a L0 e a Δθ:
ΔL = α.L0.Δθ
em que α é o coeficiente de dilatação linear.
Sendo ΔL = L - L0, vem:
L = L0(1 + α.Δθ)
Dilatação superficial
Analogamente temos:
ΔA = β.A0.Δθ e A = A0(1 + β.Δθ)
em que β é o coeficiente de dilatação superficial.
Relação:
β = 2α
Dilatação volumétrica
Analogamente temos:
ΔV = γ.V0.Δθ e V = V0(1 + γ.Δθ)
em que γ é o coeficiente de dilatação volumétrica.
Relação:
γ = 3α
Exercícios básicos
Exercício 1:
Uma lâmina bimetálica é constituída por duas tiras justapostas feitas de metais diferentes. Um dos metais (vamos chamá-lo de A) possui coeficiente de dilatação maior do que o outro (que chamaremos de B). Na temperatura ambiente a lâmina está reta. Ao ser aquecida a lâmina sofre um encurvamento. Nestas condições, o metal A constitui o arco externo ou interno da lâmina?
Resolução: clique aqui
Exercício 2:
Por que nas ferrovias os trilhos são assentados com um espaço entre eles?
Resolução: clique aqui
Exercício 3:
Numa aula de dilatação térmica o professor colocou a seguinte questão: aquece-se uma placa metálica com um furo no meio. O que ocorre com a placa e o furo? Para que os alunos discutissem o professor apresentou três possibilidades:
a) a placa e o furo dilatam.
b) a placa dilata e o furo contrai.
c) a placa contrai e o furo dilata.
Qual você escolheria como correta?
Resolução: clique aqui
Exercício 4:
Uma barra metálica de comprimento 2,0.102 cm, quando aquecida de
25 ºC a 50 ºC sofre um aumento em seu comprimento de 1,0.10-2 cm. Qual é o coeficiente de dilatação linear do material que constitui a barra?
Resolução: clique aqui
O coeficiente de dilatação superficial do alumínio é igual a 44.10-6 ºC-1. Determine o coeficiente de dilatação volumétrica do alumínio.
Resolução: clique aqui
Exercício 6:
Um bloco metálico é aquecido de 20 ºC a 120 ºC e seu volume sofre um acréscimo de 3%. Qual é o coeficiente de dilatação linear do material que constitui o bloco?
Resolução: clique aqui
segunda-feira, 27 de fevereiro de 2012
Cursos do Blog - Mecânica
Movimento Uniforme (I)
Borges e Nicolau
Movimento Progressivo
É o movimento em que o móvel caminha a favor da orientação positiva da trajetória.
No movimento progressivo os espaços crescem com o decorrer do tempo e a velocidade escalar é positiva.
Movimento Retrógrado
É o movimento em que o móvel caminha contra a orientação positiva da trajetória.
No movimento retrógrado os espaços decrescem com o decorrer do tempo e a velocidade escalar é negativa.
Movimento Uniforme (MU)
É o movimento que possui velocidade escalar constante (e não nula).
No movimento uniforme (MU) a velocidade escalar é a mesma em todos os instantes e coincide com a velocidade escalar média, qualquer que seja o intervalo de tempo considerado.
Função horária do MU
De v = Δs/Δt => v = (s-s0)/(t-0) => s-s0 = vt, vem:
Animação:
Exercícios básicos
Exercício 1:
Dê exemplos de movimentos uniformes que ocorrem no dia a dia.
Resolução: clique aqui
Exercício 2:
Um móvel realiza um movimento uniforme e seu espaço varia com o tempo segundo a tabela:
a) Classifique o movimento dizendo se é progressivo ou retrógrado.
b) Calcule e velocidade escalar do móvel.
c) Qual é o espaço inicial do móvel.
d) Escreva a função horária dos espaços.
e) Construa o gráfico s x t.
x
Resolução: clique aqui
x
Exercício 3:
Dois móveis, A e B, realizam movimentos uniformes em uma trajetória retilínea e suas funções horárias são sA = 15 + 10t (SI) e sB = 35 + 5t (SI). Determine:
a) A distância entre os móveis no instante t = 0;
b) O instante em que os móveis se encontram;
c) Os espaços dos móveis no instante do encontro;
d) Construa os gráficos, no mesmo diagrama, dos espaços dos móveis A e B em função do tempo.
Resolução: clique aqui
Exercício 4:
Dois automóveis, A e B, deslocam-se numa pista retilínea com velocidades escalares vA = 20 m/s e vB = 15 m/s. No instante t = 0 a distância entre os automóveis é de 500 m. Qual é a distância que o carro que está na frente percorre, desde o instante t = 0, até ser alcançado pelo carro de trás? Considere os carros como pontos materiais.
Resolução: clique aqui
Exercício 5:
Um trem de 300 m de comprimento atravessa completamente um túnel de 700 m de comprimento. Sabendo se que o trem realiza um movimento uniforme e que a travessia dura 1 minuto, qual é a velocidade do trem, em km/h?
Resolução: clique aqui
Exercício 6:
Dois carros, A e B, realizam movimentos uniformes. O carro A parte de São Paulo no sentido de Mairiporã e o carro B parte, no mesmo instante, no sentido de Mairiporã para São Paulo. A distância entre as duas cidades é de 42 km. A velocidade do carro A é de 80 km/h. Qual deve ser a velocidade do carro B para que os dois se cruzem a 30 km de São Paulo?
Resolução: clique aqui
Borges e Nicolau
Movimento Progressivo
É o movimento em que o móvel caminha a favor da orientação positiva da trajetória.
No movimento progressivo os espaços crescem com o decorrer do tempo e a velocidade escalar é positiva.
Movimento Retrógrado
É o movimento em que o móvel caminha contra a orientação positiva da trajetória.
No movimento retrógrado os espaços decrescem com o decorrer do tempo e a velocidade escalar é negativa.
Movimento Uniforme (MU)
É o movimento que possui velocidade escalar constante (e não nula).
No movimento uniforme (MU) a velocidade escalar é a mesma em todos os instantes e coincide com a velocidade escalar média, qualquer que seja o intervalo de tempo considerado.
Função horária do MU
De v = Δs/Δt => v = (s-s0)/(t-0) => s-s0 = vt, vem:
Animação:
Movimento Uniforme
Clique aquiExercícios básicos
Exercício 1:
Dê exemplos de movimentos uniformes que ocorrem no dia a dia.
Resolução: clique aqui
Exercício 2:
Um móvel realiza um movimento uniforme e seu espaço varia com o tempo segundo a tabela:
a) Classifique o movimento dizendo se é progressivo ou retrógrado.
b) Calcule e velocidade escalar do móvel.
c) Qual é o espaço inicial do móvel.
d) Escreva a função horária dos espaços.
e) Construa o gráfico s x t.
x
Resolução: clique aqui
x
Exercício 3:
Dois móveis, A e B, realizam movimentos uniformes em uma trajetória retilínea e suas funções horárias são sA = 15 + 10t (SI) e sB = 35 + 5t (SI). Determine:
a) A distância entre os móveis no instante t = 0;
b) O instante em que os móveis se encontram;
c) Os espaços dos móveis no instante do encontro;
d) Construa os gráficos, no mesmo diagrama, dos espaços dos móveis A e B em função do tempo.
Resolução: clique aqui
Exercício 4:
Dois automóveis, A e B, deslocam-se numa pista retilínea com velocidades escalares vA = 20 m/s e vB = 15 m/s. No instante t = 0 a distância entre os automóveis é de 500 m. Qual é a distância que o carro que está na frente percorre, desde o instante t = 0, até ser alcançado pelo carro de trás? Considere os carros como pontos materiais.
Resolução: clique aqui
Exercício 5:
Um trem de 300 m de comprimento atravessa completamente um túnel de 700 m de comprimento. Sabendo se que o trem realiza um movimento uniforme e que a travessia dura 1 minuto, qual é a velocidade do trem, em km/h?
Resolução: clique aqui
Exercício 6:
Dois carros, A e B, realizam movimentos uniformes. O carro A parte de São Paulo no sentido de Mairiporã e o carro B parte, no mesmo instante, no sentido de Mairiporã para São Paulo. A distância entre as duas cidades é de 42 km. A velocidade do carro A é de 80 km/h. Qual deve ser a velocidade do carro B para que os dois se cruzem a 30 km de São Paulo?
Resolução: clique aqui
domingo, 26 de fevereiro de 2012
Arte do Blog
A Semana de Arte Moderna
No mês de fevereiro de 1922, entre os dias 11 e 18, o Teatro Municipal de São Paulo foi palco de um evento da maior importância para a cultura brasileira. A Semana de Arte Moderna marcou a ruptura com os rígidos padrões estéticos de então. Sob vaias, apupos e alguns aplausos, aconteram conferências, apresentações musicais, discursos, declamações e performances de dança com conteúdo e formatos inovadores e polêmicos para a época.
Abaporu - Tarsila do Amaral
Mudar, subverter a produção artística, criar uma arte essencialmente brasileira, embora em sintonia com as novas tendências européias, essa era basicamente a intenção dos modernistas. Na Semana de 22 despontaram talentos como os de Mário e Oswald de Andrade na literatura, Víctor Brecheret na escultura e Anita Malfatti na pintura.
Revista Klaxon
A Semana, como toda inovação, não foi bem acolhida pelos tradicionais paulistas. A elite, habituada a modelos estéticos europeus mais arcaicos, sentiu-se violentada em sua sensibilidade e afrontada em suas preferências artísticas.
Di Cavalcanti
O propósito dos modernistas foi atingido. Com Di Cavalcanti como um dos organizadores, a Semana de Arte Moderna foi propositadamente pensada para chocar.
Oswald de Andrade
Vaiando e gritando impropérios os conservadores engoliram sem saborear um programa que entre outras coisas apresentou uma leitura de poema por Oswald de Andrade, um discurso sobre estética por Mário de Andrade, uma conferência sobre arte e estética por Menotti del Picchia, a leitura do poema “Os Sapos” de Manuel Bandeira. Além de um recital de Villa-Lobos.
Anita Malfatti
A partir da Semana de Arte Moderna de 1922 deu-se o rompimento da nova geração de artistas e intelectuais brasileiros com o academicismo, o parnasianismo e o simbolismo. Podemos dizer que a Semana propiciou a renovação estética no Brasil, criando padrões que embora inspirados no que acontecia na Europa, foram deglutidos e transubstanciados em linguagem tropical. Os reflexos na sociedade brasileira, a partir de 1930, são perceptíveis não só nas artes plásticas, mas também na música, na arquitetura e, principalmente, no comportamento. Já não havia estranheza na contemplação de bananeiras em jardins de mansões, antes ornados exclusivamente por arbustos importados da Europa.
sábado, 25 de fevereiro de 2012
Especial de Sábado
Ganhadores do Premio Nobel de Física
Borges e Nicolau
x
1938
Enrico Fermi, pela descoberta de novos elementos radioativos produzidos por irradiação de nêutrons e pela descoberta de reações nucleares induzidas por nêutrons lentos.
Enrico Fermi, nasceu em 1901, em Roma, Itália. Inúmeras foram suas contribuições para o desenvolvimento da Física Nuclear. Explicou o decaimento beta; produziu radioatividade artificial bombardeando substâncias diferentes com nêutrons; descobriu que esse processo tornava-se mais eficaz por ação de nêutrons lentos; construiu o primeiro reator a fissão nuclear na Universidade de Chicago.
Em 1938 Enrico Fermi foi distinguido com o premio Nobel de Física. Faleceu em 1954, em Chicago, EUA.
“Há dois resultados possíveis: Se o resultado confirma a hipótese, então você fez uma medição. Se o resultado é contrário à hipótese, então você fez uma descoberta”.
Próximo Sábado: Ganhador do Premio Nobel de 1939:
Ernest Orlando Lawrence, pela invenção do cíclotron.
sexta-feira, 24 de fevereiro de 2012
quinta-feira, 23 de fevereiro de 2012
Caiu no vestibular
Fios elétricos
(UFF-RJ)
Considere dois pedaços de fios cilíndricos A e B, do mesmo comprimento, feitos de um mesmo material, com diâmetros distintos, porém, pequenos demais para serem medidos diretamente. Para comparar as espessuras dos dois fios, mediu-se a corrente I que atravessa cada fio como função de diferença de potencial à qual está submetido. Os resultados estão representados na figura.
Analisando os resultados, conclui-se que a relação entre os diâmetros d dos fios A e B é
(A) dA = 2dB.
(B) dA = dB/2.
(C) dA = 4dB.
(D) dA = dB/4.
(E) dA = √2dB.
Resolução:
U = RA.IA => 10 = [(ρ.L)/(π.dA2/4)].1,00 (1)
U = RB.IB => 10 = [(ρ.L)/(π.dB2/4)].0,25 (2)
De (1) e (2):
[(ρ.L)/(π.dA2/4)].1,00 = [(ρ.L)/(π.dB2/4)].0,25 => dA = 2dB.
Resposta: (A)
(UFF-RJ)
Considere dois pedaços de fios cilíndricos A e B, do mesmo comprimento, feitos de um mesmo material, com diâmetros distintos, porém, pequenos demais para serem medidos diretamente. Para comparar as espessuras dos dois fios, mediu-se a corrente I que atravessa cada fio como função de diferença de potencial à qual está submetido. Os resultados estão representados na figura.
Analisando os resultados, conclui-se que a relação entre os diâmetros d dos fios A e B é
(A) dA = 2dB.
(B) dA = dB/2.
(C) dA = 4dB.
(D) dA = dB/4.
(E) dA = √2dB.
Resolução:
U = RA.IA => 10 = [(ρ.L)/(π.dA2/4)].1,00 (1)
U = RB.IB => 10 = [(ρ.L)/(π.dB2/4)].0,25 (2)
De (1) e (2):
[(ρ.L)/(π.dA2/4)].1,00 = [(ρ.L)/(π.dB2/4)].0,25 => dA = 2dB.
Resposta: (A)
quarta-feira, 22 de fevereiro de 2012
Desafio de Mestre (Especial)
Hoje é dia 22 de fevereiro e, conforme combinado, estamos publicando a resolução do Desafio de Mestre (Especial). O ganhador do livro foi o leitor Rangel.
Borges e Nicolau
Atravessando o rio
Atravessando o rio
A velocidade da correnteza em relação às margens (velocidade de arrastamento) tem módulo de 4,0 m/s e a velocidade do barco em relação às águas (velocidade relativa) tem o mínimo módulo possível. Determine o módulo da velocidade relativa e o módulo da velocidade do barco em relação às margens (velocidade resultante).
Dados: sen 30º = 1/2; sen 60º = √3/2.
Lembre-se que:
Resolução:
A velocidade resultante vres tem a direção da reta AB e o sentido de A para B. A velocidade de arrastamento varr tem a direção e o sentido da correnteza. A velocidade relativa vrel tem módulo mínimo quando for perpendicular à reta AB:
No triângulo sombreado temos:
sen 30º = vrel/varr => 1/2 = vrel/4,0 => vrel = 2,0 m/s
cos 30º = vres/varr => √3/2 = vres/4,0 => vres = 2,0.√3 m/s
Cursos do Blog - Eletricidade
Processos de eletrização (II)
x
Borges e Nicolau
xEletrização por Indução
O condutor A (indutor) eletrizado positivamente é aproximado do condutor B (induzido), inicialmente neutro. As cargas do induzido separam-se devido às interações eletrostáticas. Cargas negativas são atraídas pelas cargas positivas do indutor e cargas positivas são repelidas.
Ligando-se o induzido à Terra, as cargas positivas são neutralizadas por cargas negativas (elétrons) que fluem da Terra através da ligação. No induzido ficam apenas cargas negativas.
O processo é finalizado desligando-se o induzido da Terra e afastando-se o indutor.
O induzido (B) inicialmente neutro está finalmente eletrizado com carga de sinal contrário à do indutor (A).
O processo pode ser feito com o indutor carregado com cargas negativa. Nesse caso o induzido ficará carregado positivamente.
Corpo eletrizado atraindo um corpo neutro
Por indução um corpo eletrizado pode atrair um corpo neutro.
As cargas positivas de A atraem as negativas de B e repelem as positivas de B. A força de atração tem intensidade maior do que a de repulsão.
Animação:
Eletrização por indução
Clique aqui
Observação: Ao abrir o link da UFRGS você encontrará a animação: "eletrização por contato". Proceda de acordo com as instruções abaixo para encontrar a eletrização por indução.
Quadro 1
Exercícios básicos
Exercício 1:
Quando uma esfera metálica A eletrizada negativamente é aproximada de outra esfera metálica B, inicialmente neutra, ocorre o fenômeno da indução eletrostática. Faça um desenho representando a esfera A (eletrizada negativamente), a esfera B e as cargas elétricas induzidas em B.
Resolução: clique aqui
Exercício 2:
Qual é a sequência dos procedimentos que devem ser seguidos para que B fique eletrizado? O sinal da carga elétrica que B adquire é o mesmo de A?
Resolução: clique aqui
Um bastão de borracha, eletrizado positivamente, é aproximado de duas esferas metálicas, A e B, que estão em contato. A seguir, afasta-se ligeiramente uma esfera da outra e remove-se o bastão de borracha. Por último, as esferas são suficientemente afastadas de modo que uma não exerça influência na outra. Faça um esquema da distribuição de cargas elétricas induzidas nas esferas A e B nas situações:
a) Bastão próximo às esferas que estão em contato:
b) Esferas são ligeiramente afastadas e o bastão é removido:
c) Esferas são muito afastadas uma da outra
Resolução: clique aqui
Exercício 4:
Numa aula de Eletrostática, o professor coloca a seguinte situação: são dadas três esferas metálicas A, B e C. Observa-se que B atrai A e B repele C. No que diz respeito ao estado de eletrização das esferas, o professor apresenta quatro possibilidades e pede aos alunos que escolham aquelas compatíveis com as observações:
Qual ou quais você escolheria?
Resolução: clique aqui
Exercício 5:
Uma barra de vidro depois de atritada com um pano de lã atrai pequenos pedaços de papel. Como você explicaria este fato, sabendo-se que o papel é um isolante?
Resolução: clique aqui
terça-feira, 21 de fevereiro de 2012
Cursos do Blog - Termologia, Óptica e Ondas
Termometria (II)
Na semana passada iniciamos o estudo de Termometria. Vamos continuar com este assunto. Reveja o resumo teórico da aula passada e resolva, a seguir, os exercícios.
As escalas Celsius e Fahrenheit
Na escala Celsius, adotam-se os valores 0 ºC e 100 ºC para o ponto de gelo e para o ponto de vapor, respectivamente.
Na escala Fahrenheit, adotam-se os valores 32 ºF e 212 ºF para o ponto de gelo e para o ponto de vapor, respectivamente.
Conversão entre a temperatura Celsius (θC) e a temperatura Fahrenheit (θF)
Relação entre a variação de temperatura na escala Celsius (ΔθC) e na escala Fahrenheit (ΔθF)
A escala absoluta Kelvin
A escala absoluta Kelvin adota a origem no zero absoluto, estado térmico em que cessaria a agitação térmica. Sua unidade (kelvin: K) tem extensão igual à do grau Celsius (ºC).
Relação entre a temperatura Kelvin (T) e a Celsius (θC)
Relação entre as variações de temperatura
Exercícios básicos
Exercício 1:
O físico alemão Daniel Gabriel Fahrenheit* (1686-1736) construiu seus próprios termômetros e em 1714 passou a usar o mercúrio como substância termométrica. A escala que leva seu nome foi criada em 1724, adotando como “zero” uma mistura de gelo, água e sal de amônia e 96 para a temperatura do corpo humano. Posteriormente fez ajustes em sua escala, atribuindo os valores 32 e 212, respectivamente, para os pontos de congelamento e ebulição da água, sob pressão normal. Medidas mais precisas indicam que a temperatura média do corpo humano é da ordem de 98,6 ºF.
As temperaturas de 0 ºF e 98,6 ºF correspondem, respectivamente, nas escalas Celsius* e Kelvin* aos valores:
a) -17,8 ºC e 310 K
b) -17,8 ºC e 371,6 K
c) -32 ºC e 273 K
d) 0 ºC e 318,6 K
e) 8 ºC e 37 K
*Siga os links e saiba mais.
Resolução: clique aqui
Exercício 2:
Uma escala E adota os valores 15 °E para o ponto do gelo e 105 °E para o ponto do vapor. Qual é a indicação dessa escala que corresponde à temperatura de 72 °F?
Resolução: clique aqui
Resposta: 35 º E
Exercício 3:
A variação de temperatura de 108 °F equivale a:
a) 42 °C b) 84 °C c) 108 °C d) 60 K e) 333 K
Resolução: clique aqui
Exercício 4:
A temperatura indicada por um termômetro graduado na escala Fahrenheit excede em duas unidades o triplo da indicação de outro termômetro graduado na escala Celsius. Qual é esta temperatura medida na escala Kelvin?
Resolução: clique aqui
Exercício 5:
Antigamente foi usada uma escala absoluta, criada pelo engenheiro e físico escocês Willian John Maquorn Rankine* (1820-1872), que adotava como unidade o grau Rankine (°Ra), cuja extensão era igual à do grau Fahrenheit (ºF) e que considerava o zero absoluto como 0 ºRa.
Determine:
a) a temperatura do zero absoluto na escala Fahrenheit;
b) a relação entre a temperatura absoluta Rankine (TR) e a temperatura Fahrenheit correspondente (θF);
c) os valores das temperaturas correspondentes ao ponto do gelo e ao ponto do vapor na escala absoluta Rankine.
*Siga o link e saiba mais.
Resolução: clique aqui
Borges e Nicolau
Na semana passada iniciamos o estudo de Termometria. Vamos continuar com este assunto. Reveja o resumo teórico da aula passada e resolva, a seguir, os exercícios.
As escalas Celsius e Fahrenheit
Na escala Celsius, adotam-se os valores 0 ºC e 100 ºC para o ponto de gelo e para o ponto de vapor, respectivamente.
Na escala Fahrenheit, adotam-se os valores 32 ºF e 212 ºF para o ponto de gelo e para o ponto de vapor, respectivamente.
Conversão entre a temperatura Celsius (θC) e a temperatura Fahrenheit (θF)
Relação entre a variação de temperatura na escala Celsius (ΔθC) e na escala Fahrenheit (ΔθF)
A escala absoluta Kelvin
A escala absoluta Kelvin adota a origem no zero absoluto, estado térmico em que cessaria a agitação térmica. Sua unidade (kelvin: K) tem extensão igual à do grau Celsius (ºC).
Relação entre a temperatura Kelvin (T) e a Celsius (θC)
Relação entre as variações de temperatura
Exercícios básicos
Exercício 1:
O físico alemão Daniel Gabriel Fahrenheit* (1686-1736) construiu seus próprios termômetros e em 1714 passou a usar o mercúrio como substância termométrica. A escala que leva seu nome foi criada em 1724, adotando como “zero” uma mistura de gelo, água e sal de amônia e 96 para a temperatura do corpo humano. Posteriormente fez ajustes em sua escala, atribuindo os valores 32 e 212, respectivamente, para os pontos de congelamento e ebulição da água, sob pressão normal. Medidas mais precisas indicam que a temperatura média do corpo humano é da ordem de 98,6 ºF.
As temperaturas de 0 ºF e 98,6 ºF correspondem, respectivamente, nas escalas Celsius* e Kelvin* aos valores:
a) -17,8 ºC e 310 K
b) -17,8 ºC e 371,6 K
c) -32 ºC e 273 K
d) 0 ºC e 318,6 K
e) 8 ºC e 37 K
*Siga os links e saiba mais.
Resolução: clique aqui
Exercício 2:
Uma escala E adota os valores 15 °E para o ponto do gelo e 105 °E para o ponto do vapor. Qual é a indicação dessa escala que corresponde à temperatura de 72 °F?
Resolução: clique aqui
Resposta: 35 º E
Exercício 3:
A variação de temperatura de 108 °F equivale a:
a) 42 °C b) 84 °C c) 108 °C d) 60 K e) 333 K
Resolução: clique aqui
Exercício 4:
A temperatura indicada por um termômetro graduado na escala Fahrenheit excede em duas unidades o triplo da indicação de outro termômetro graduado na escala Celsius. Qual é esta temperatura medida na escala Kelvin?
Resolução: clique aqui
Exercício 5:
Antigamente foi usada uma escala absoluta, criada pelo engenheiro e físico escocês Willian John Maquorn Rankine* (1820-1872), que adotava como unidade o grau Rankine (°Ra), cuja extensão era igual à do grau Fahrenheit (ºF) e que considerava o zero absoluto como 0 ºRa.
Determine:
a) a temperatura do zero absoluto na escala Fahrenheit;
b) a relação entre a temperatura absoluta Rankine (TR) e a temperatura Fahrenheit correspondente (θF);
c) os valores das temperaturas correspondentes ao ponto do gelo e ao ponto do vapor na escala absoluta Rankine.
*Siga o link e saiba mais.
Resolução: clique aqui
segunda-feira, 20 de fevereiro de 2012
Cursos do Blog - Mecânica
Velocidade escalar média e velocidade escalar instantânea
Borges e Nicolau
Introdução
Para o cálculo da velocidade média que um carro desenvolve numa viagem basta dividir a distância que o carro percorre, ao longo da estrada, pelo intervalo de tempo contado desde a partida até a chegada. Por exemplo, um carro parte de São Paulo (capital) às 8 h da manhã e chega a Guaxupé (MG) ao meio dia, após percorrer
320 km. Para calcular a velocidade média desenvolvida dividimos 320 km por 4 h. Encontramos: 320 km/4 h = 80 km/h. Observe que o carro se desloca sempre no mesmo sentido e não ocorre inversão do movimento ao longo da estrada. É assim que estamos acostumados no nosso dia a dia: dividimos a distância percorrida pelo intervalo de tempo gasto.
Vamos agora ampliar esta definição, considerando a trajetória descrita por um móvel, em relação a um certo referencial. Seja s1 o espaço do móvel num instante t1 e s2 seu espaço num instante posterior t2. Seja Δs = s2 - s1 a variação de espaço no intervalo de tempo Δt = t2 - t1.
A seguir, vamos definir velocidade escalar média do móvel no intervalo de tempo Δt para uma variação de espaço Δs qualquer. Para o cálculo de Δs devemos levar em conta apenas as posições inicial e final, mesmo ocorrendo inversão no sentido do movimento.
Velocidade escalar média:
Sendo Δs > 0, isto é, s2 > s1, resulta Vm > 0. Se não houver inversão no sentido do movimento a variação de espaço Δs coincide com a distância efetivamente percorrida pelo móvel ao longo da trajetória (figura 1).
Se Δs < 0, temos Vm < 0 (figura 2).
No caso em que Δs = 0, resulta Vm = 0 (figura 3)
Unidades de velocidade: cm/s; m/s; km/h
Sendo 1 km = 1000 m e 1 h = 3600 s, vem :
1 km/h = 1000 m/3600 s = (1/3,6) m/s. Portanto: 1 m/s = 3,6 km/h
Vamos analisar alguns exemplos:
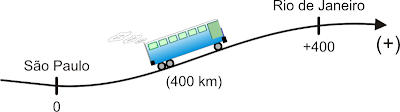
Um ônibus vai de São Paulo ao Rio de Janeiro em cinco horas, enquanto outro ônibus faz o percurso inverso, do Rio de Janeiro a São Paulo também em cinco horas. Vamos determinar a velocidade escalar média de cada veículo, sabendo que a distância entre Rio de Janeiro e São Paulo é de 400 quilômetros.
Precisamos inicialmente definir um sentido de percurso, isto é, orientar a trajetória e escolher uma das cidades como origem dos espaços (marco zero).
Assim, supondo que São Paulo seja a origem dos espaços, a ela será atribuído o marco zero. Como a distância entre as cidades é de 400 km, ao Rio de Janeiro caberá o marco +400, sendo o sentido adotado de São Paulo para o Rio de Janeiro.
Vamos então calcular a velocidade escalar média de cada um dos veículos, o primeiro indo de São Paulo ao Rio e o segundo fazendo o percurso inverso, Rio-São Paulo.
Veículo 1 => São Paulo-Rio
Espaço da partida s1 = 0 (partiu da origem do espaços, km 0)
Espaço da chegada s2 = 400 km
Variação de espaço: Δs = s2 - s1 = 400 km – 0 = 400 km
Duração da viagem Δt = 5h
Cálculo da velocidade escalar média vm
vm = Δs/Δt => vm = 400 km/5 h => vm = 80 km/h
Veículo 2 => Rio – São Paulo
Espaço da partida s1 = 400 km
Espaço da chegada s2 = 0
Variação de espaço: Δs = s2 - s1 = 0 - 400 km = -400 km
Duração da viagem ∆t = 5h
Cálculo da velocidade escalar vm
vm = Δs/Δt => vm = -400 km/5 h => vm = -80 km/h
Como você notou, em uma das viagens um dos veículos apresentou velocidade escalar média negativa, o que ocorreu em função da orientação da trajetória.
Imagine um terceiro exemplo, mantendo a origem dos espaços em São Paulo e orientando a trajetória de São Paulo para o Rio.
Um ônibus sai de São Paulo, vai ao Rio de Janeiro e volta pela mesma estrada, chegando a Resende, situada no km 260. Qual é a velocidade escalar média do ônibus entre São Paulo e Resende sabendo-se que todo percurso foi realizado em 6,5 horas?
Espaço da partida s1 = 0
Espaço da chegada s2 = 260 km
Variação de espaço: Δs = s2 - s1 = 260 km - 0 = 260 km
Duração da viagem - Intervalo de tempo (∆t) => ∆t = 6,5 h
Cálculo da velocidade escalar vm
vm = Δs/Δt => vm = 260 km/6,5 h => vm = 40 km/h
Observação: É assim que procedemos em Física: adotamos um ponto como origem dos espaços, orientamos a trajetória, determinamos as posições inicial e final do móvel e o intervalo de tempo gasto no percurso.
No caso em questão, como acabamos de calcular, a velocidade escalar média entre São Paulo e Resende resultou em 40 km/h.
Se você calculasse efetivamente a distância percorrida pelo ônibus neste trajeto encontraria de São Paulo ao Rio de Janeiro e do Rio de Janeiro a Resende as distâncias 400 km e 140 km, cuja soma é igual a 540 km, o que levaria a uma velocidade média de 540 km/6,5 h, aproximadamente 83 km/h. Está não é a velocidade escalar média definida em Física.
Algumas considerações:
1) Quando, num determinado percurso, o móvel não inverte o sentido do movimento e se desloca no sentido em que a trajetória foi orientada, a distância efetivamente percorrida (d) e a variação de espaço (Δs) são numericamente iguais.
2) No cálculo da velocidade escalar média só interessam os instantes da partida e da chegada.
Veja este exemplo:
Um carro parte de São Paulo às 08h00 da manhã e chega ao Rio de Janeiro às 13h00. O motorista parou para almoçar, tendo ficado no restaurante durante uma hora.
Ao efetuarmos o cálculo da velocidade escalar média, não nos interessa o que aconteceu durante o percurso (almoço) e sim o intervalo de tempo entre a partida e a chegada.
A velocidade escalar média vm, portanto, foi de 80 km/h. E, desde que os instantes de partida e chegada permanecessem iguais, a vm continuaria a mesma, ainda que o almoço tivesse durado 2 horas. Ou, quem sabe, 3 horas!
Animação:
Velocidade escalar média
Clique aqui
Velocidade escalar instantânea:
A velocidade escalar num instante é indicada por v e pode ser entendida como sendo a velocidade escalar média tomada em um intervalo de tempo Δt extremamente pequeno, com Δt tendendo a zero, ou seja, t2 tendendo a t1.
O velocímetro de um carro fornece a velocidade escalar instantânea, isto é, indica a velocidade do carro em cada instante.
Exercícios Básicos
Exercício 1:
Um atleta percorre a distância de 100 m em 10 s. Qual é a velocidade escalar média do atleta? Dê a resposta em km/h e m/s.
Resolução: clique aqui
Exercício 2:
A velocidade escalar média de uma pessoa em passo normal é de 1,5 m/s. Quanto tempo a pessoa gasta para fazer uma caminhada de 3 km?
Resolução: clique aqui
Exercício 3:
É dada a função horária do movimento de um móvel s = 8 - 6t + t2, sendo o espaço s medido em metros e o instante t em segundos. Determine a velocidade escalar média do móvel entre os instantes:
a) 1 s e 2 s
b) 2 s e 4 s
c) 5 s e 6 s
Resolução: clique aqui
Exercício 4:
A distância entre as cidades de Goiânia e de Caldas Novas é de 169 km. Um ônibus parte de Goiânia às 13h e chega à cidade de Caldas Novas às 15h10min, tendo feito uma parada de 10min num posto de abastecimento.
Qual é a velocidade escalar média desenvolvida pelo ônibus nesse trajeto?
Resolução: clique aqui
Exercício 5:
Numa viagem de João Pessoa a Cabedelo, uma moto desenvolve a velocidade escalar média de 80 km/h até a metade do percurso e de 60 km/h na metade seguinte.
Qual é a velocidade escalar média desenvolvida pela moto de João Pessoa a Cabedelo?
Resolução: clique aqui
Exercício 6:
A função horária da velocidade de um móvel é dada por v = 5 - 2t, para v em m/s e t em s. Determine:
a) a velocidade do móvel nos instante 0 e 2 s.
b) em que instante a velocidade escalar do móvel se anula?
Resolução: clique aqui
Borges e Nicolau
Introdução
Para o cálculo da velocidade média que um carro desenvolve numa viagem basta dividir a distância que o carro percorre, ao longo da estrada, pelo intervalo de tempo contado desde a partida até a chegada. Por exemplo, um carro parte de São Paulo (capital) às 8 h da manhã e chega a Guaxupé (MG) ao meio dia, após percorrer
320 km. Para calcular a velocidade média desenvolvida dividimos 320 km por 4 h. Encontramos: 320 km/4 h = 80 km/h. Observe que o carro se desloca sempre no mesmo sentido e não ocorre inversão do movimento ao longo da estrada. É assim que estamos acostumados no nosso dia a dia: dividimos a distância percorrida pelo intervalo de tempo gasto.
Vamos agora ampliar esta definição, considerando a trajetória descrita por um móvel, em relação a um certo referencial. Seja s1 o espaço do móvel num instante t1 e s2 seu espaço num instante posterior t2. Seja Δs = s2 - s1 a variação de espaço no intervalo de tempo Δt = t2 - t1.
A seguir, vamos definir velocidade escalar média do móvel no intervalo de tempo Δt para uma variação de espaço Δs qualquer. Para o cálculo de Δs devemos levar em conta apenas as posições inicial e final, mesmo ocorrendo inversão no sentido do movimento.
Velocidade escalar média:
vm = Δs/Δt
Sendo Δs > 0, isto é, s2 > s1, resulta Vm > 0. Se não houver inversão no sentido do movimento a variação de espaço Δs coincide com a distância efetivamente percorrida pelo móvel ao longo da trajetória (figura 1).
Figura 1
Se Δs < 0, temos Vm < 0 (figura 2).
Figura 2
No caso em que Δs = 0, resulta Vm = 0 (figura 3)
Figura 3
Unidades de velocidade: cm/s; m/s; km/h
Sendo 1 km = 1000 m e 1 h = 3600 s, vem :
1 km/h = 1000 m/3600 s = (1/3,6) m/s. Portanto: 1 m/s = 3,6 km/h
Vamos analisar alguns exemplos:
Um ônibus vai de São Paulo ao Rio de Janeiro em cinco horas, enquanto outro ônibus faz o percurso inverso, do Rio de Janeiro a São Paulo também em cinco horas. Vamos determinar a velocidade escalar média de cada veículo, sabendo que a distância entre Rio de Janeiro e São Paulo é de 400 quilômetros.
Precisamos inicialmente definir um sentido de percurso, isto é, orientar a trajetória e escolher uma das cidades como origem dos espaços (marco zero).
Assim, supondo que São Paulo seja a origem dos espaços, a ela será atribuído o marco zero. Como a distância entre as cidades é de 400 km, ao Rio de Janeiro caberá o marco +400, sendo o sentido adotado de São Paulo para o Rio de Janeiro.
Vamos então calcular a velocidade escalar média de cada um dos veículos, o primeiro indo de São Paulo ao Rio e o segundo fazendo o percurso inverso, Rio-São Paulo.
Veículo 1 => São Paulo-Rio
Espaço da partida s1 = 0 (partiu da origem do espaços, km 0)
Espaço da chegada s2 = 400 km
Variação de espaço: Δs = s2 - s1 = 400 km – 0 = 400 km
Duração da viagem Δt = 5h
Cálculo da velocidade escalar média vm
vm = Δs/Δt => vm = 400 km/5 h => vm = 80 km/h
Veículo 2 => Rio – São Paulo
Espaço da partida s1 = 400 km
Espaço da chegada s2 = 0
Variação de espaço: Δs = s2 - s1 = 0 - 400 km = -400 km
Duração da viagem ∆t = 5h
Cálculo da velocidade escalar vm
vm = Δs/Δt => vm = -400 km/5 h => vm = -80 km/h
Como você notou, em uma das viagens um dos veículos apresentou velocidade escalar média negativa, o que ocorreu em função da orientação da trajetória.
Imagine um terceiro exemplo, mantendo a origem dos espaços em São Paulo e orientando a trajetória de São Paulo para o Rio.
Um ônibus sai de São Paulo, vai ao Rio de Janeiro e volta pela mesma estrada, chegando a Resende, situada no km 260. Qual é a velocidade escalar média do ônibus entre São Paulo e Resende sabendo-se que todo percurso foi realizado em 6,5 horas?
Espaço da partida s1 = 0
Espaço da chegada s2 = 260 km
Variação de espaço: Δs = s2 - s1 = 260 km - 0 = 260 km
Duração da viagem - Intervalo de tempo (∆t) => ∆t = 6,5 h
Cálculo da velocidade escalar vm
vm = Δs/Δt => vm = 260 km/6,5 h => vm = 40 km/h
Observação: É assim que procedemos em Física: adotamos um ponto como origem dos espaços, orientamos a trajetória, determinamos as posições inicial e final do móvel e o intervalo de tempo gasto no percurso.
No caso em questão, como acabamos de calcular, a velocidade escalar média entre São Paulo e Resende resultou em 40 km/h.
Se você calculasse efetivamente a distância percorrida pelo ônibus neste trajeto encontraria de São Paulo ao Rio de Janeiro e do Rio de Janeiro a Resende as distâncias 400 km e 140 km, cuja soma é igual a 540 km, o que levaria a uma velocidade média de 540 km/6,5 h, aproximadamente 83 km/h. Está não é a velocidade escalar média definida em Física.
Algumas considerações:
1) Quando, num determinado percurso, o móvel não inverte o sentido do movimento e se desloca no sentido em que a trajetória foi orientada, a distância efetivamente percorrida (d) e a variação de espaço (Δs) são numericamente iguais.
2) No cálculo da velocidade escalar média só interessam os instantes da partida e da chegada.
Veja este exemplo:
Um carro parte de São Paulo às 08h00 da manhã e chega ao Rio de Janeiro às 13h00. O motorista parou para almoçar, tendo ficado no restaurante durante uma hora.
Ao efetuarmos o cálculo da velocidade escalar média, não nos interessa o que aconteceu durante o percurso (almoço) e sim o intervalo de tempo entre a partida e a chegada.
A velocidade escalar média vm, portanto, foi de 80 km/h. E, desde que os instantes de partida e chegada permanecessem iguais, a vm continuaria a mesma, ainda que o almoço tivesse durado 2 horas. Ou, quem sabe, 3 horas!
Animação:
Velocidade escalar média
Clique aqui
Velocidade escalar instantânea:
A velocidade escalar num instante é indicada por v e pode ser entendida como sendo a velocidade escalar média tomada em um intervalo de tempo Δt extremamente pequeno, com Δt tendendo a zero, ou seja, t2 tendendo a t1.
O velocímetro de um carro fornece a velocidade escalar instantânea, isto é, indica a velocidade do carro em cada instante.
Exercícios Básicos
Exercício 1:
Um atleta percorre a distância de 100 m em 10 s. Qual é a velocidade escalar média do atleta? Dê a resposta em km/h e m/s.
Resolução: clique aqui
Exercício 2:
A velocidade escalar média de uma pessoa em passo normal é de 1,5 m/s. Quanto tempo a pessoa gasta para fazer uma caminhada de 3 km?
Resolução: clique aqui
Exercício 3:
É dada a função horária do movimento de um móvel s = 8 - 6t + t2, sendo o espaço s medido em metros e o instante t em segundos. Determine a velocidade escalar média do móvel entre os instantes:
a) 1 s e 2 s
b) 2 s e 4 s
c) 5 s e 6 s
Resolução: clique aqui
Exercício 4:
A distância entre as cidades de Goiânia e de Caldas Novas é de 169 km. Um ônibus parte de Goiânia às 13h e chega à cidade de Caldas Novas às 15h10min, tendo feito uma parada de 10min num posto de abastecimento.
Qual é a velocidade escalar média desenvolvida pelo ônibus nesse trajeto?
Resolução: clique aqui
Exercício 5:
Numa viagem de João Pessoa a Cabedelo, uma moto desenvolve a velocidade escalar média de 80 km/h até a metade do percurso e de 60 km/h na metade seguinte.
Qual é a velocidade escalar média desenvolvida pela moto de João Pessoa a Cabedelo?
Resolução: clique aqui
Exercício 6:
A função horária da velocidade de um móvel é dada por v = 5 - 2t, para v em m/s e t em s. Determine:
a) a velocidade do móvel nos instante 0 e 2 s.
b) em que instante a velocidade escalar do móvel se anula?
Resolução: clique aqui
Assinar:
Postagens (Atom)