Resoluções
de Mecânica
1.
Após se destacar da
mesa, desprezando-se a resistência do ar, a bolinha fica sob ação exclusiva de
seu peso e terá uma trajetória parabólica pois resulta da composição de um
movimento horizontal uniforme com um movimento vertical uniformemente variado.
Resposta: D
2.
Sendo a força constante a trajetória será parabólica e a
componente da velocidade na direção perpendicular à
força permanece
constante. Após desligar os propulsores o foguete terá movimento retilíneo e
uniforme.
Resposta: C
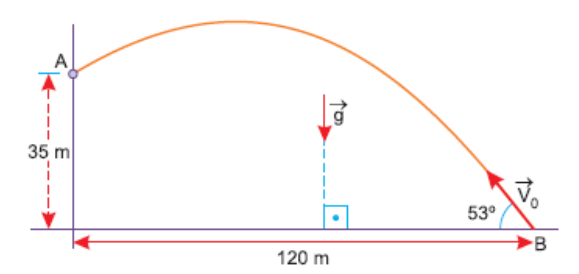
3.
Na direção horizontal:
Sx = V0x. t
120 = V0 cos 53° . T
120 = 0,6 V0 T ⇒ (1)
Na direção vertical:
Sy = V0y t + t2
35 = (V0 sen 53°) T – 5,0 T2
35 = V0 . 0,8T – 5,0T2 (2)
(1) em (2): 35 = 200 . 0,8 – 5,0 T2
5,0T2 = 160 – 35 = 125
T2 = 25 (SI) ⇒T=5,0s
Na relação (1):
V0 . 5,0 = 200=>V0 =40 m/s
Resposta: C
4. Cálculo do tempo de voo:
Sy = V0y
t +10 t2 /2
1 = 0 + 5T2=>T =(1/5)1/2 s
Cálculo do módulo da velocidade inicial:
SX = V0x
t=>3=V0 . (1/5)1/2=>V0=3.(5)1/2M/S
Cálculo do alcance vertical com lançamento com
o
mesmo módulo de V0:
V2=(V0)2+2
(–10) H
0 = 9 . 5 + 2 (–10) H
20H = 45=>H=2,25 m
Resposta: B
5.
A força de atrito que
a parede exerce na moeda de R$ 1,00
deve equilibrar o peso
do conjunto:
Fat = P1 +
P2 = 0,14N
Resposta: E
6.
A varredura reduz o
coeficiente de atrito cinético entre a
pedra e o piso e com
isto a força de atrito sobre a pedra
diminui e o seu retardamento
também diminui.
Resposta: B
7.
A balança de pratos
sempre indica a massa real do corpo
e não depende do valor
do módulo da aceleração da
gravidade local e
portanto:
m1 = 5,0 kg
e m3 = 5,0 kg
2) A balança de
plataforma (balança de mola) mede a força
de compressão que o
corpo aplica sobre sua plataforma
e portanto sua
indicação depende da aceleração da
gravidade local.
A balança B só indica
a massa real do corpo quando for
usada no local onde
foi calibrada.
Na situação 1 como a
gravidade é menor, a força de
compressão sobre a
plataforma é menor e a indicação da
balança é menor que a
massa real, isto é, m2 < 5,0 kg.
Na situação 2 não foi
especificado se o elevador está
subindo com movimento
acelerado ou retardado.
Se o movimento for acelerado
(pretendido pelo
examinador) o vetor
aceleração é dirigido para cima e a
gravidade aparente
dentro do elevador é maior que a
real: gap = g + a e a
força de compressão na plataforma
é maior que o peso
real e a indicação da balança B é
maior que a massa
real, isto é, m4 > 5,0 kg.
Se o movimento for
retardado, então o vetor aceleração
é dirigido para baixo
a gravidade aparente dentro do
elevador é menor que a
real: gap = g – a e a balança B
marca menos que a
massa real, isto é, m4 < 5,0 kg.
Das opções
apresentadas apenas a alternativa A pode
ser possível desde que
o movimento de subida do
elevador seja
acelerado.
Resposta: A
8.
No movimento de queda,
é sabido que a aceleração da
gravidade é a mesma
para todos os corpos.
No experimento do segundo
aluno a mesma folha cai em
tempos diferentes,
pois, ao amassá-la, o colega B altera a
área de contato entre
o papel e o ar. Assim, altera a força
de resistência do ar
sobre a folha de papel.
Resposta: B
9.
Para que não haja
escorregamento, a força motora não
pode superar a força
de atrito de destaque.
Fmotora < ou = Fatdestaque
Fmotora < ou = μE FN
200 < ou = μE . 800 => μE >ou= 200/800=0,25
Com exceção do
cimento, todos os demais revestimentos
seriam adequados,
porém o mais econômico é a madeira.
Resposta: C
10.
O conceito de Potência
nos remete à taxa de transferência
de energia cinética,
isto é, a razão entre a energia cinética
e o tempo gasto para
obtê-la.
De 0 a 100km/h a
variação de energia cinética é a mesma,
porém, o tempo gasto
pela versão à álcool é menor (12,9s)
e, portanto, o carro à
álcool desenvolve maior potência.
Resposta: C
11.
Conservação da energia
mecânica:
Eelástica =
Ecinética=> k.x.x/2=mv.v/2=>v=x. (k/m)1/2
Mantendo a mesma mola
(k = constante), o módulo da
velocidade de
lançamento é proporcional à deformação x
da mola. Para que V
seja multiplicada por 4, então x deverá
ser multiplicado por
4.
Resposta: B
12.
Conservação da energia
mecânica entre A e B:
EB = EA (referência em
B)
= MgR
Na posição B a resultante é centrípeta:
2Tmáx – PB = Fcp
2Tmáx – Mg = 2Mg
2Tmáx = 3Mg
Tmáx =((3/2) .( 24 .
10) (N) =360 N
De acordo com o texto:
Truptura = 1,25 Tmáx =
1,25 . 360N=450N
Resposta: D
13.
A força que acelera o carrinho
é a força de atrito que o solo
rugoso aplica em suas
rodas.
O atrito é do tipo
estático porque as rodas não estão
deslizando. Cumpre
contudo ressaltar que a força de atrito
não realiza trabalho.
São as forças internas do carrinho que
transformam energia
elástica em cinética.
Resposta: B
14.
Devido ao trabalho da
força de resistência do ar, há
transformação de
energia cinética do meteorito em energia
térmica, tornando-o
incandescente e com brilho intenso.
A energia cinética Ec
= está associada à grande
velocidade do
meteorito.
Resposta: C
15.
Conservação da energia
mecânica:
Efinal = Einicial
Como a velocidade
escalar linear é desprezível em com -
paração com a
velocidade escalar angular, então a energia
final é exclusivamente
a energia cinética de rotação:
Ecinrotação
= Einicial = mg h
Ecinrotação
= 30 . 10–3
. 10 . 0,410 (J)
Ecinrotação
= 0,820 .10-1J
Resposta: B
16.
De acordo com o texto
as unidades a fio d’água geram
energia associada à
vazão de água do rio que, por sua vez,
é função crescente da
velocidade da correnteza.
Para uma área A de
secção transversal do leito do rio a
vazão Z é dada por:
Z = A . V
V = módulo da
velocidade da correnteza
Resposta : A
18.
Cálculo do módulo da
velocidade de impacto entre o
tijolo e o capacete:
Conservação da energia
mecânica:
Como P = mg = 25N,
então:
mgh= mv2/2=>g.h
= v2/2 =>10.5,0= v2/2=>v=10m/s
Pelo teorema do
impulso e admitindo que imediatamente após o
impacto a velocidade
do tijolo seja nula, temos pelo teorema do impulso:
Iresultante =
m(v-vo). considerando que a força impulsiva
média se referisse à
força resultante média sobre o tijolo.
F. t=m.v
F= mv/t
F= 2,5.10/0,5(N) = 50N=2P
Resposta: A
Nota: Considerando a
força resultante F-P não teríamos alternativa correta.
Resoluções de
eletricidade
1.
Q = i t
Q = 1500mAh
Q = 1500 . 10–3A
. 3600s
Q = 5400 A.s = 5400C
Resposta: C
2.
Na situação proposta,
temos:
imáx = 1000
mA = 1 A
imáx =Q/t
1000mA=4000mAh/t=> t
=4h
Resposta: C
3.
Para evitarmos um
acidente com uma pessoa encostando
na cerca de arame
farpado, esta deverá ser aterrada, pois
seus fios de arame
passarão a ter potencial zero volt,
igualando-se ao da
terra. Deste modo, a ddp (diferença de
potencial) se anula e
a pessoa não leva choque elétrico
Resposta:A
4.
Ao dividirmos a tensão
elétrica (V) pela intensidade de
corrente elétrica (i),
obtemos a resistência elétrica aparente
R (Lei de Ohm).
Assim, sendo:
V=10i +1,0i2
Portanto:V/i=(10i+1,0i2)/i
=>R=10+1,0i
Concluímos, dessa
maneira, que a resistência elétrica apa -
rente (R) varia com a
intensidade de corrente elétrica (i) de
acordo com uma função
do primeiro grau. Portanto, o
gráfico é um reta.
O coeficiente linear
da função é 10 e o coeficiente angular
é 1,0. Assim, o
gráfico correspondente é o da alternativa D.
Resposta: D
5.
As duas baterias podem
ser associadas em série ou
paralelo, resultando
respectivamente nas forças
eletromotrizes E1 e
E2:
E1 = 24V
E2 = 12V
Para a pele molhada,
temos R = 1kΩ = 1.103 Ω
Da Primeira Lei de Ohm,
temos:
i1 = 24/1.103
A=24mA
i2 = 12/1.103
A=12mA
De tabela, a parada
respiratória se dá para correntes
elétricas entre 20mA e
100mA, condição atendida
com a corrente elétrica i1,
ou seja, para a associação
em série das baterias,
apresentada na alternativa A.
Resposta A
6.
Com os dados
fornecidos na tabela e utilizando-se a
2.a Lei de Ohm _R = ρ.L/A=, temos:
R1 = ρ. 34,7
R2 = ρ.11,75
R3 = ρ.27
R4 = ρ.106
Observando-se os
valores encontrados, temos:R2<R3<R1<R4
Resposta: C
7.
Usando a Primeira Lei
de Ohm, resulta para as rotas 1,2 e 3:
Rota1
R1=510(J/carro.m)/4(carro/s)=127,5(J.s/carro2.m)
Rota 2:
R2 =(608/4)(J.s/carro2.m)=152(J.s/carro2.m)
Rota 3:
R3 =(575/3) (J.s/carro2.m)=191,67(J.s/carro2.m)
Ordenando de maneira
crescente, temos:R1<R2<R3
Resposta A
8.
↓
Fechando o circuito no
ponto A, temos o seguinte: os dois resistores de 4kΩ ficam ligados em paralelo (resistor
equivalente 2kΩ) que fica em série com o resistor de 4kΩ, pois o circuito
está aberto em B. A resistência total do circuito é igual a:
Req = 2kΩ + 4kΩ = 6kΩ
Resposta: C
9.
Calculemos, inicialmente, a resistência
elétrica total do fio:
R = ρ.L/A=1,7.10-8.28/4.10-6=>R=11,9.10-2Ω
10.
11. No circuito dado,
temos:

12.
Observando-se o
circuito e os terminais da fonte ora
designados por x e y,
temos:
A lâmpada A queimada
atua como circuito aberto e
consequentemente B
também apaga. A lâmpada D
continua apagada, pois
está em curto-circuito.
A lâmpada C continua
acesa com o mesmo brilho, pois está
ligada diretamente aos
terminais da fonte.
Resposta: B
13.
Antes de ligar o
equipamento, os quatro resistores idên -
ticos receberão do
gerador, cada um, uma tensão elétrica:
U1= = 3,0V
Assim, para se obter
os 9,0V necessários para o funcio -
namento do seu
equipamento, basta usar 3 resistores
consecutivos.
Podem-se usar os
terminais (A e D) ou (B e E).
Ao se ligar o
equipamento, cuja resistência elétrica vale R =
10k_, ele será percorrido por uma corrente elétrica de
intensidade:
i2 = ⇒ i2= =
i2 = 0,9 . 10–3A ⇒
Nota:
A rigor, a tensão
elétrica entre B e E é aproximada mente de
9,0V.
Há um desvio de
corrente i2 para o equipamento, mas seu
valor é muito pequeno,
em comparação com a intensidade
da corrente i
fornecida pelo gerador.
Resposta: D
Resoluções de Termologia
1.
Potência total gerada = 800W
Calor de aquecimento da água e da tigela:
Q = Qa + Qt = ma caΔθ + mt ctΔθ
Q = 500 . 1,0 . 34 +
300 . 0,2 . 34 (cal)
Q = 17000 cal +
2040cal = 19 040 cal
Q = 19 040 . 4,2J =
79968J
Cálculo da potência
útil:
Potu= Q/Δt= 79968J/2,5 . 60s=
533,12W
Cálculo do rendimento R:
R=Potu/ Pottotal=533,12/800
= 0,6664 (66,6%)
Resposta: D
2.
Volumes iguais de
concreto e de água deverão receber a
mesma quantidade de energia
térmica por incidência de
radiação solar.
Qconcreto = Qágua
(mc_Δθ)concreto = (mcá(mc_Δθ)água
gua
2500 . 0,8 Δθ C = 1000 .
4,2 Δθ A
2000 . Δθ C = 4200 Δθ A
Δθ C/ Δθ A= 4200/2000 = 2,1
Resposta: B
3.
Dados:
Pot = 50W
t = 1,0h = 3600s
μ =m/ V
m = μ. V
m = (1,0kg /L) . (50L)
m = 50kg
c = 4,0 kJ/ kg. K =
4000J/ kg .K
A partir da potência
da fonte térmica, calculamos a variação
de temperatura:
Pot =m.c. Δ θ/ Δt
50=50.4000. Δ θ/3600
Δ θ = 0,9K =0,9°C
Resposta: C
4.
Cálculo do calor de combustão
da castanha-de-caju:
C = 70K cal/10g = 7000cal/g
Cálculo do calor total
produzido pela queima de 2,5g de
castanha-de-caju:
QT = m. C =
2,5g. 7000cal/g =17500 cal
Cálculo do calor útil
para aquecer a água com 50% do calor
total:
Q = 0,50. QT
= 0,50. 17 500 cal= 8750 cal
Cálculo da temperatura
final (θ) para aquecer 350g de água
(c = 1 cal /g.°C) a
partir de 20°C:
Q = m.c.(θ-20)=350.1.(θ -20)=8750=>
θ-20=8750/350=25
θ -20 =25=> θ=45°C
Resposta: C
5.
O modo mais eficiente
de aquecer a água é através da convecção
térmica e para isso a água deve entrar
na posição mais baixa
(3) e sair na posição mais alta (4).
Resposta: D
6.
O fluxo de calor por
condução através das paredes dos
recipientes A e B, em forma
de paralelepípedos, é calcu -
lado pela Lei de
Fourier:
ϕ =Q/ Δt = k. A. Δ θ/e
No caso do recipiente A, Q = mLF e A= 2ab + 2ac + 2bc
mLF/
Δt=(2.40.40 +2.40.40
+2.40.40) Δ θ/e = kA.9600. Δ θ/e (1)
Recipiente B:
2mLF/Δ t = kB.(2.60.40 +2.60.40
+2.40.40) Δ θ/e = kB12800. Δ θ/e (2)
mLF/Δ t = kB6400. Δ θ/e (3)
igualando-se os segundos membros de (1) e (3),resulta:
kA/kB=6400/9600= -
Resposta: B
7.
A energia térmica flui
espontaneamente da maior para a
menor temperatura,
logo, “frio não entra”, como propõe o
jingle.
A porta da casa
minimiza as perdas de calor do interior da
casa para o exterior,
enquanto o cobertor proporciona um
bom isolamento térmico
entre o corpo da pessoa e o am -
biente do dormitório,
reduzindo a condução do calor para
o ambiente.
Resposta: C
8.
O início da saída de
vapores pela válvula da panela é um
indicador de que a
água entrou em ebulição no interior da
mesma, o que
geralmente ocorre acima de 100°C devido à
maior pressão sobre a
água.
Durante a ebulição, a
temperatura da água permanece
constante. Por isso, é
recomendável abaixar a intensidade
da chama, evitando-se
com isso o consumo desnecessário
de gás.
A manutenção da chama
do fogão com maior intensidade
faz apenas com que a
água vaporize mais rapidamente
dentro da panela.
Resposta:
9.
1) Na primeira
situação a jarra pintada de preto absorve ca -
lor mais rapidamente
que a pintada de branco e atinge
a temperatura ambiente
em um tempo menor.
2) Na segunda situação
a jarra pintada de preto irradia ca -
lor mais rapidamente
que a pintada de branco e atinge
a temperatura ambiente
em um tempo menor.
Resposta: A
10.
O incômodo mencionado
pelo personagem da tirinha deve--se
ao fato de que, em
dias úmidos, o suor tem maior
dificuldade para
evaporar do corpo e retirar calor da pele
para refrescá-la.
Resposta: B
ol e a ilha de calor é
a irradiação e, entre a ilha de calor e
a brisa marítima, é a
convecção das massas de ar.
Resposta: A