Mecânica - Aula 26 (continuação)

Exercícios de Revisão

 
Revisão/Ex 1:
Um bloco de massa 5,0 kg encontra-se em repouso sobre  uma mesa. Os coeficientes de atrito estático e dinâmico entre o bloco e a mesa são, respectivamente, 0,50 e 0,40. Considere g = 10 m/s². Uma força horizontal de intensidade F é aplicada no bloco.

a) Em que intervalo pode variar a intensidade F, da força horizontal aplicada, para que o bloco permaneça em repouso?
b) Qual a intensidade da força de atrito nos casos F = 10 N e F = 30 N. 

Resolução: clique aqui

Revisão/Ex 2:
(FUVEST)
O sistema indicado na figura a seguir, onde as polias são ideais, permanece em repouso graças a força de atrito entre o corpo de 10 kg e a superfície de apoio.

Podemos afirmar que o valor da força de atrito é (g=10 m/s²):
a) 20 N
b) 10 N
c) 100 N
d) 60 N
e) 40 N

Resolução: clique aqui

Revisão/Ex 3:
(UFG-GO)
Um catador de recicláveis de massa m sobe uma ladeira empurrando seu carrinho. O coeficiente de atrito estático entre o piso e os seus sapatos e μe e o ângulo que a ladeira forma com a horizontal e θ. O carrinho, por estar sobre rodas, pode ser considerado livre de atrito. A maior massa do carrinho com os recicláveis que ele pode suportar, sem escorregar, e de
 
a) m.[μ_e.(sen θ/cos θ) - 1] 
b) m.(μ_e.cos θ - sen θ) 
c) m.[μ_e - (cos θ/sen θ)] 
d) m.(μ_e.sen θ - cos θ) 
e) m.[μ_e.(cos θ/sen θ) - 1]

Resolução: clique aqui

Revisão/Ex 4:
(PUC-PR)
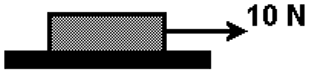
A figura representa um corpo de massa 10 kg apoiado em uma superfície horizontal. O coeficiente de atrito entre as superfícies em contato é 0,4. Em determinado instante, é aplicado ao corpo uma força horizontal de 10 N. 

Considere g = 10 m/s² e marque a alternativa correta:

a) A força de atrito atuante sobre o corpo é 40 N.
b) A velocidade do corpo decorridos 5 s é 10 m/s.
c) A aceleração do corpo é 5 m/s².
d) A aceleração do corpo é 2 m/s² e sua velocidade decorridos 2 s é 5 m/s.
e) O corpo não se movimenta e a força de atrito é 10 N.

Resolução: clique aqui

Revisão/Ex 5:
(PUC-RS)
Um professor pretende manter um apagador parado, pressionando-o contra o quadro de giz (vertical). Considerando P o peso do apagador, e o coeficiente de atrito entre as superfícies do apagador e a do quadro igual a 0,20, a força mínima aplicada, perpendicular ao apagador, para que este fique parado, é

a) 0,20.P. 
b) 0,40.P. 
c) 1,0.P. 
d) 2,0.P. 
e) 5,0.P.

Resolução: clique aqui

Desafio:

No esquema os blocos A e B estão em equilíbrio. O fio que liga os blocos forma com a horizontal um ângulo θ. Considere o fio e a polia ideais.

Dados:

Coeficiente de atrito estático entre o bloco A e o plano horizontal: μ = 0,50
Peso do bloco A: P_A = 60 N.
sen θ = 0,80; cos θ = 0,60
 
Para haver equilíbrio o peso de B(P_B) é tal que:

a) 0 ≤ P_B ≤ 30 N
b) 0 ≤ P_B ≤ 60 N
c) 0 ≤ P_B ≤ 90 N
d) P_B ≥ 60 N
e) P_B ≥ 30 N

A resolução será publicada na próxima quinta-feira.

Resolução do desafio anterior:

Na figura 1, um bloco de massa m é lançado com velocidade v₀ do topo A de um plano inclinado, atingindo o ponto B do plano, com velocidade nula. Considere dados: o coeficiente de atrito μ entre o bloco e o plano, sen θ, cos θ e a velocidade v₀. Determine a velocidade v com que o bloco deve ser lançado de B, para que atinja o ponto A com velocidade nula (figura 2).

Resolução:

PFD:
F_at - P_t = m.a₁
μmgcos θ - mgsen θ = ma₁
a1 = g(μcos θ - sen θ)

Equação de Torricelli

0 = v₀² - 2a₁.AB
v₀² = 2a₁.AB (1)

 
PFD:
F_at + P_t = m.a₂
μmgcos θ + mgsen θ = ma₂
a₂ = g(μcos θ + sen θ)

Equação de Torricelli

0 = v² - 2a₂.AB
v² = 2a₂.AB (2)

De (1) e (2):

v = v₀.(a₂/a₁)^1/2

v = v₀.[(μcos θ + sen θ)/(μcos θ - sen θ)]^1/2