Borges e Nicolau
1. (UECE)
Dois trechos sucessivos de uma estrada retilínea são percorridos por um automóvel da seguinte maneira: no 1.° trecho ele percorre 150 km a 100 km/h e no 2.° trecho, percorre 60 km a 60 km/h. No percurso total a velocidade média do automóvel, em km/h, é igual a
A) 96
B) 90
C) 84
D) 80
Resolução:
vm = Δs/Δt
No 1º trecho: 100 = 150/Δt1 => Δt1 = 150/100 => Δt1 = 1,5 h
No 2º trecho: 60 = 60/Δt2 => Δt2 = 60/60 => Δt2 = 1,0 h
No percurso total: vm = (150 + 60)/(Δt1 + Δt2) => vm = 210/2,5 =>
vm = 84 km/h
Alternativa: C
2. (UFLA-MG)
vm = Δs/Δt
No 1º trecho: 100 = 150/Δt1 => Δt1 = 150/100 => Δt1 = 1,5 h
No 2º trecho: 60 = 60/Δt2 => Δt2 = 60/60 => Δt2 = 1,0 h
No percurso total: vm = (150 + 60)/(Δt1 + Δt2) => vm = 210/2,5 =>
vm = 84 km/h
Alternativa: C
2. (UFLA-MG)
Um objeto move-se com velocidade constante e percorre 80 cm em 2 s. Um estudante, ao analisar o movimento, faz a razão entre os números 2 e 80, obtendo o valor 0,025. A interpretação CORRETA desse valor é:
A) O objeto demora 1 s para percorrer 0,025 cm.
B) Esse valor representa a velocidade do objeto.
C) Esse valor representa a aceleração do objeto.
D) O objeto demora 0,025 s para percorrer 1 cm.
Resolução:
vm = v = Δs/Δt
v = 80/2 cm/s => v = 40 cm/s
1 s => 40 cm
t s => 1 cm
t = 0,025 s
Alternativa: D
3. (UESPI)
vm = v = Δs/Δt
v = 80/2 cm/s => v = 40 cm/s
1 s => 40 cm
t s => 1 cm
t = 0,025 s
Alternativa: D
3. (UESPI)
Um carro A inicia seu movimento retilíneo a partir do repouso, no instante t = 0, com uma aceleração constante igual a 0,5 m/s2. Neste mesmo instante, passa por ele um carro B, que se desloca na mesma direção e no mesmo sentido do carro A, porém com velocidade escalar constante igual a 3,0 m/s. Considerando tal situação, qual é o tempo necessário para que o carro A alcance o carro B?
A) 6 s
B) 10 s
C) 12 s
D) 15 s
E) 20 s
Resolução:
Carro A:xxxxxxxxxxxxxxCarro B:
s0 = 0xxxxxxxxxxxxxxxxxs0 = 0
v0 = 0xxxxxxxxxxxxxxxXxv = 3,0 m/s
α = 0,5 m/s2
Funções horárias
sA = 0,25.t2 => sB = 3,0.t
No instante do encontro sA = sB
0,25.t2 = 3,0 t => 0,25 t = 3,0 => t = 3,0/0,25 =>
t = 12 s
Alternativa: C
4. (FUVEST-SP)
Carro A:xxxxxxxxxxxxxxCarro B:
s0 = 0xxxxxxxxxxxxxxxxxs0 = 0
v0 = 0xxxxxxxxxxxxxxxXxv = 3,0 m/s
α = 0,5 m/s2
Funções horárias
sA = 0,25.t2 => sB = 3,0.t
No instante do encontro sA = sB
0,25.t2 = 3,0 t => 0,25 t = 3,0 => t = 3,0/0,25 =>
t = 12 s
Alternativa: C
4. (FUVEST-SP)
Dirigindo-se a uma cidade próxima, por uma autoestrada plana, um motorista estima seu tempo de viagem, considerando que consiga manter uma velocidade média
dex90 km/h. Ao ser surpreendido pela chuva, decide reduzir sua velocidade média para 60 km/h, permanecendo assim até a chuva parar, quinze minutos mais tarde, quando retoma sua velocidade média inicial. Essa redução temporária aumenta seu tempo de viagem, com relação à estimativa inicial, em
dex90 km/h. Ao ser surpreendido pela chuva, decide reduzir sua velocidade média para 60 km/h, permanecendo assim até a chuva parar, quinze minutos mais tarde, quando retoma sua velocidade média inicial. Essa redução temporária aumenta seu tempo de viagem, com relação à estimativa inicial, em
A) 5 minutos.
B) 7,5 minutos.
C) 10 minutos.
D) 15 minutos.
E) 30 minutos.
Resolução:
Em 15 min = (1/4) h, com velocidade de 60 km/h o motorista percorre a distância:
Δs = v.Δt => Δs = 60 (km/h).1/4(h) = 15 km
Se mantivesse a velocidade de 90 km/h, teria percorrido os 15 km num intervalo de tempo:
Δt = Δs/v => Δt = 15 km/90 km = (1/6) h = 10 min
Nestas condições, o tempo de viagem aumentou de:
15 min - 10 min = 5 min.
Alternativa: A
5. (UFV-MG)
Em 15 min = (1/4) h, com velocidade de 60 km/h o motorista percorre a distância:
Δs = v.Δt => Δs = 60 (km/h).1/4(h) = 15 km
Se mantivesse a velocidade de 90 km/h, teria percorrido os 15 km num intervalo de tempo:
Δt = Δs/v => Δt = 15 km/90 km = (1/6) h = 10 min
Nestas condições, o tempo de viagem aumentou de:
15 min - 10 min = 5 min.
Alternativa: A
5. (UFV-MG)
Um veículo, movendo-se em linha reta, desacelera uniformemente, a partir
de 72 km/h, parando em 4,0 s. A distância percorrida pelo veículo e o módulo de sua velocidade média durante a desaceleração são, respectivamente:
de 72 km/h, parando em 4,0 s. A distância percorrida pelo veículo e o módulo de sua velocidade média durante a desaceleração são, respectivamente:
A) 40 m e 10 m/s.
B) 80 m e 20 m/s.
C) 20 m e 5 m/s.
D) 20 m e 20 m/s.
Resolução:
72 km/h = 72/3,6 m/s = 20 m/s
α = Δv/Δt => α = -20/4,0 => α = -5,0 m/s2
Aplicando Torricelli:
v2 = (v0)2 + 2.α.ΔS
0 = 202 -2.5,0.Δs => 10.Δs = 400 => Δs = 40 m
vm = Δs/Δt = 40/4,0 => vm = 10 m/s
Alternativa: A
6. (UFCG-PB)
72 km/h = 72/3,6 m/s = 20 m/s
α = Δv/Δt => α = -20/4,0 => α = -5,0 m/s2
Aplicando Torricelli:
v2 = (v0)2 + 2.α.ΔS
0 = 202 -2.5,0.Δs => 10.Δs = 400 => Δs = 40 m
vm = Δs/Δt = 40/4,0 => vm = 10 m/s
Alternativa: A
6. (UFCG-PB)
É dever de todo/a cidadão/ã respeitar as regras de trânsito, a vida própria e a dos outros, o que não faz um motorista alcoolizado à direção. Como exemplo, considere um motorista viajando a 72 km/h que observando o sinal vermelho, aplica instantaneamente os freios, e para em 10 segundos, justamente na borda da faixa de pedestres. Suponha que, num outro dia, cometendo a imprudência de consumir bebida alcoólica e dirigir e viajando à mesma velocidade e exatamente na mesma estrada e no mesmo ponto, ele observa a mudança de cor do sinal para o vermelho. Acontece que agora ele demora 0,20 segundo até aplicar os freios. Considerando que o carro freie com a mesma aceleração anterior, pode-se afirmar que avança sobre a faixa de pedestre
A) 1,0 m.
B) 4,0 m.
C) 2,0 m.
D) 5,0 m.
E) 6,0 m.
Resolução:
A distância percorrida pelo carro no intervalo de tempo igual a 0,20 s corresponde ao espaço invadido da faixa. Assim:
v = 72 km/h => 72/3,6 m/s => v = 20 m/s
v = Δs/Δt => 20 = Δs/0,20 => Δs = 4,0 m
Alternativa: B
7. (CEFET-SP)
A distância percorrida pelo carro no intervalo de tempo igual a 0,20 s corresponde ao espaço invadido da faixa. Assim:
v = 72 km/h => 72/3,6 m/s => v = 20 m/s
v = Δs/Δt => 20 = Δs/0,20 => Δs = 4,0 m
Alternativa: B
7. (CEFET-SP)
O crescente aumento do número de veículos automotores e o consequente aumento de engarrafamentos têm levado a Prefeitura do Município de São Paulo a um monitoramento intensivo das condições de circulação nas vias da cidade. Em uma sondagem, um funcionário da companhia de trânsito deslocou seu veículo, constatando que
– permaneceu parado, durante 30 minutos;
– movimentou-se com velocidade de 20 km/h, durante 12 minutos;
– movimentou-se com velocidade de 45 km/h, durante 6 minutos.
Da análise de seus movimentos, pôde-se constatar que, para o deslocamento realizado, a velocidade média desenvolvida foi, em km/h,
A) 10,5.
B) 12,0.
C) 13,5.
D) 15,0.
E) 17,5.
Resolução:
vm = Δs/Δt
1) permaneceu parado durante 30 minutos =>
Δs1 = 0; Δt1 = 30 minutos => Δt1 = 1/2 h
2) movimentou-se com v = 20 km/h durante 12 minutos =>
20 = Δs2/1/5 (12 minutos = 1/5 h) =>
Δs2 = 4 km; Δt2 = 1/5 h
3) movimentou-se com v = 45 km/h durante 6 minutos =>
45 = Δs3/1/10 (6 minutos = 1/10 h) =>
Δs3 = 4,5 km; Δt3 = 1/10 h
vm = (Δs1 + Δs2 + Δs3)/(Δt1 + Δt2 + Δt3) =>
vm = (0 + 4 + 4,5)/(1/2 + 1/5 + 1/10)
vm = 8,5/0,8 => 10,625 km/h ≈ 11 km/h
Alternativa: A
8. (AFA-SP)
vm = Δs/Δt
1) permaneceu parado durante 30 minutos =>
Δs1 = 0; Δt1 = 30 minutos => Δt1 = 1/2 h
2) movimentou-se com v = 20 km/h durante 12 minutos =>
20 = Δs2/1/5 (12 minutos = 1/5 h) =>
Δs2 = 4 km; Δt2 = 1/5 h
3) movimentou-se com v = 45 km/h durante 6 minutos =>
45 = Δs3/1/10 (6 minutos = 1/10 h) =>
Δs3 = 4,5 km; Δt3 = 1/10 h
vm = (Δs1 + Δs2 + Δs3)/(Δt1 + Δt2 + Δt3) =>
vm = (0 + 4 + 4,5)/(1/2 + 1/5 + 1/10)
vm = 8,5/0,8 => 10,625 km/h ≈ 11 km/h
Alternativa: A
8. (AFA-SP)
O gráfico da posição (S) em função do tempo (t) a seguir representa o movimento retilíneo de um móvel.
A partir do gráfico é correto afirmar que,
A) no primeiro segundo, o seu movimento é progressivo.
B) entre 1 s e 3 s, a aceleração é negativa.
C) no instante 2 s, a velocidade do móvel é nula.
D) nos instantes 1 s e 3 s, os vetores velocidades são iguais.
Resolução:
Analisando as alternativas:
A) no primeiro segundo os espaços decrescem com o tempo, o móvel caminha no sentido oposto ao da orientação da trajetória. O movimento é retrógrado. (alternativa falsa)
B) entre 1 s e 3 s a aceleração é positiva, a concavidade da curva está voltada para cima. (alternativa falsa)
C) A partir do instante t = 2 s o móvel inverte o sentido do movimento,
portanto em t = 2 s, v = 0. (alternativa correta)
D) Nos instantes 1 s e 3 s os vetores velocidade têm sentidos opostos e, portanto, não são iguais. (alternativa falsa)
Alternativa: C
9. (UFAM)
Analisando as alternativas:
A) no primeiro segundo os espaços decrescem com o tempo, o móvel caminha no sentido oposto ao da orientação da trajetória. O movimento é retrógrado. (alternativa falsa)
B) entre 1 s e 3 s a aceleração é positiva, a concavidade da curva está voltada para cima. (alternativa falsa)
C) A partir do instante t = 2 s o móvel inverte o sentido do movimento,
portanto em t = 2 s, v = 0. (alternativa correta)
D) Nos instantes 1 s e 3 s os vetores velocidade têm sentidos opostos e, portanto, não são iguais. (alternativa falsa)
Alternativa: C
9. (UFAM)
Dois automóveis A e B partem simultaneamente de um mesmo ponto e suas velocidades em função do tempo são mostradas no mesmo gráfico a seguir.
A distância que separa os móveis após 8 s é:
A) 12 m
B) 6 m
C) 10 m
D) 5 m
E) 8 m
Resolução:
Distância percorrida pelo móvel A (área em vermelho) => 40 m
Distância percorrida pelo móvel B (área em azul) => 48 m
Após 8 s a distância que separa os móveis é igual a 8 metros.
Alternativa: E
10. (UFAM)
Distância percorrida pelo móvel A (área em vermelho) => 40 m
Distância percorrida pelo móvel B (área em azul) => 48 m
Após 8 s a distância que separa os móveis é igual a 8 metros.
Alternativa: E
10. (UFAM)
A figura representa o gráfico da velocidade em função do tempo do movimento de um corpo lançado verticalmente para cima com velocidade inicial
v0 = 12 m/s, na superfície de um planeta.
A altura máxima atingida pelo corpo vale:
A) 72 m
B) 36 m
C) 144 m
D) 64 m
E) 24 m
Resolução:
No instante t = 6 s a velocidade do corpo é igual a zero e, portanto, ele está na altura máxima. A distância percorrida no intervalo de tempo de 0 s a 6 s é igual à área sob a curva. H = (6.12)/2 => H = 36 m
Alternativa: B
Resolução:
No instante t = 6 s a velocidade do corpo é igual a zero e, portanto, ele está na altura máxima. A distância percorrida no intervalo de tempo de 0 s a 6 s é igual à área sob a curva. H = (6.12)/2 => H = 36 m
Alternativa: B
11. (UNIRIO)
O gráfico abaixo mostra o comportamento de um motorista, testando seu carro novo. Ele parte do repouso de um sinal, imprimindo ao carro uma aceleração constante sem saber que a 200 m à sua frente existe um “pardal” que multa, fotografando carros com velocidades superiores a 54 km/h. Aos dez segundos, após a arrancada e com velocidade de 35 m/s, ele percebe a presença do “pardal”.
Sobre a situação proposta, podemos afirmar que
A) quando ele percebe o “pardal”, ele já foi multado.
B) quando ele percebe o “pardal”, ele se encontra a 20 m do mesmo.
C) com essa velocidade, 35 m/s, ele pode passar que não será multado.
D) para não ser multado, ele deve imprimir ao seu carro uma desaceleração
de 20 m/s2.
de 20 m/s2.
E) para não ser multado, ele deve imprimir ao seu carro uma desaceleração
de 3,5 m/s2.
de 3,5 m/s2.
Resolução:
Ao perceber o "pardal" o motorista havia percorrido: Δs = (10.35)/2 =>
Ao perceber o "pardal" o motorista havia percorrido: Δs = (10.35)/2 =>
Δs = 175 m (área sob a curva do gráfico v x t). Restavam, portanto, 25 m para reduzir a velocidade de 35 m/s para 15 m/s e escapar da multa. Para isso a aceleração deveria ser:
v2 = (v0)2 + 2.α.Δs => 152 = 352 + 2.α.25 => 225 = 1225 + 50.α
50.α = -1000 => α = -20 m/s2. O sinal (-) significa desaceleração.
Alternativa: D
12. (PUC-RIO)
v2 = (v0)2 + 2.α.Δs => 152 = 352 + 2.α.25 => 225 = 1225 + 50.α
50.α = -1000 => α = -20 m/s2. O sinal (-) significa desaceleração.
Alternativa: D
12. (PUC-RIO)
Um veleiro deixa o porto navegando 70 km em direção leste. Em seguida, para atingir seu destino, navega mais 100 km na direção nordeste. Desprezando a curvatura da terra e admitindo que todos os deslocamentos são coplanares, determine o deslocamento total do veleiro em relação ao porto de origem.
(Considere √2 = 1,40 e √5 = 2,20)
A) 106 km
B) 34 km
C) 154 km
D) 284 km
E) 217 mm
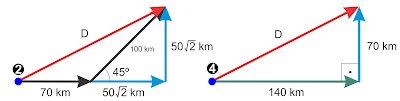
Resolução:
Da figura 4:
D2 = (140)2 + (70)2 => D2 = 19600 + 4900 => D2 = 5. 4900
D = 70√5 => D = 70.2,20 => D = 154 km
Alternativa: C
13. (AFA-SP)
Da figura 4:
D2 = (140)2 + (70)2 => D2 = 19600 + 4900 => D2 = 5. 4900
D = 70√5 => D = 70.2,20 => D = 154 km
Alternativa: C
13. (AFA-SP)
Um carro percorre uma curva circular com velocidade linear constante de 15 m/s completando-a em 5√2 s, conforme figura abaixo.
É correto afirmar que o módulo da aceleração vetorial média experimentada pelo carro nesse trecho, em m/s2, é
A) 0
B) 1,8
C) 3,0
D) 5,3
A) 0
B) 1,8
C) 3,0
D) 5,3
Resolução:
Da figura:
IΔVI2 = IV1I2 + IV2I2 => IΔVI2 = 152 + 152 => IΔVI2 = 225 + 225 =>
IΔVI2 = 2.225 => IΔVI = 15.√2
O módulo da aceleração vetorial média (am) é dado por:
IamI = IΔVI/Δt => IamI = 15.√2/5.√2 =>
IamI = 3,0 m/s2
Alternativa: C
14. (PUC-RIO)
Uma bola é lançada verticalmente para cima, a partir do solo, e atinge uma altura máxima de 20 m. Considerando a aceleração da gravidade g = 10 m/s2, a velocidade inicial de lançamento e o tempo de subida da bola são:
A) 10 m/s e 1 s
B) 20 m/s e 2 s
C) 30 m/s e 3 s
D) 40 m/s e 4 s
E) 50 m/s e 5 s
Da figura:
IΔVI2 = IV1I2 + IV2I2 => IΔVI2 = 152 + 152 => IΔVI2 = 225 + 225 =>
IΔVI2 = 2.225 => IΔVI = 15.√2
O módulo da aceleração vetorial média (am) é dado por:
IamI = IΔVI/Δt => IamI = 15.√2/5.√2 =>
IamI = 3,0 m/s2
Alternativa: C
14. (PUC-RIO)
Uma bola é lançada verticalmente para cima, a partir do solo, e atinge uma altura máxima de 20 m. Considerando a aceleração da gravidade g = 10 m/s2, a velocidade inicial de lançamento e o tempo de subida da bola são:
A) 10 m/s e 1 s
B) 20 m/s e 2 s
C) 30 m/s e 3 s
D) 40 m/s e 4 s
E) 50 m/s e 5 s
Resolução:
De H = 20 m, tiramos v0 aplicando Torricelli:
v2 = (v0)2 - 2.g.H => 02 = (v0)2 - 2.10.20 => (v0)2 = 400 =>
v0 = 20 m/s
Tempo de subida => Na altura máxima v = 0:
v = v0 - g.t => 0 = 20 - 10.t => 10.t = 20 =>
t = 2 s
Alternativa: B
15. (VUNESP)
Em um aparelho simulador de queda livre de um parque de diversões, uma pessoa devidamente acomodada e presa a uma poltrona é abandonada a partir do repouso de uma altura h acima do solo. Inicia-se então um movimento de queda livre vertical, com todos os cuidados necessários para a máxima segurança da pessoa. Se g é a aceleração da gravidade, a altura mínima a partir da qual deve-se iniciar o processo de frenagem da pessoa, com desaceleração constante 3g, até o repouso no solo é
A) h/8.
B) h/6.
C) h/5.
D) h/4.
E) h/2.
De H = 20 m, tiramos v0 aplicando Torricelli:
v2 = (v0)2 - 2.g.H => 02 = (v0)2 - 2.10.20 => (v0)2 = 400 =>
v0 = 20 m/s
Tempo de subida => Na altura máxima v = 0:
v = v0 - g.t => 0 = 20 - 10.t => 10.t = 20 =>
t = 2 s
Alternativa: B
15. (VUNESP)
Em um aparelho simulador de queda livre de um parque de diversões, uma pessoa devidamente acomodada e presa a uma poltrona é abandonada a partir do repouso de uma altura h acima do solo. Inicia-se então um movimento de queda livre vertical, com todos os cuidados necessários para a máxima segurança da pessoa. Se g é a aceleração da gravidade, a altura mínima a partir da qual deve-se iniciar o processo de frenagem da pessoa, com desaceleração constante 3g, até o repouso no solo é
A) h/8.
B) h/6.
C) h/5.
D) h/4.
E) h/2.
Resolução:
Do ponto de altura h até o ponto A da figura a poltrona cai sob a ação da gravidade g. Velocidade no ponto A:
(vA)2 = 02 + 2.g.y => (vA)2 = 2.g.y (1)
Do ponto A até o solo (vs = 0) a poltrona é desacelerada com -3g:
(vs)2 = (vA)2 - 2.3.g.x (x = distância de A ao solo)
0 = (vA)2 - 2.3.g.x => (vA)2 = 6.g.x (2)
Substituindo-se (1) em (2), vem:
2.g.y = 6.g.x => 6.x = 2.y => 3x = y (3)
x + y = h => x + 3.x = h => 4x = h => x = h/4
Alternativa: D
16. (FEI-SP)
Da calçada, João atira para cima uma pequena esfera de vidro com
velocidade de 20 m/s. No mesmo instante, Pedro solta uma esfera igual de uma altura de 50 m acima do ponto de lançamento. Em que altura acima do ponto de lançamento as duas esferas se encontraram pela 1ª vez?
A) 18,75 m
B) 32,25 m
C) 25,00 m
D) 30,00 m
E) 15,25 m
Do ponto de altura h até o ponto A da figura a poltrona cai sob a ação da gravidade g. Velocidade no ponto A:
(vA)2 = 02 + 2.g.y => (vA)2 = 2.g.y (1)
Do ponto A até o solo (vs = 0) a poltrona é desacelerada com -3g:
(vs)2 = (vA)2 - 2.3.g.x (x = distância de A ao solo)
0 = (vA)2 - 2.3.g.x => (vA)2 = 6.g.x (2)
Substituindo-se (1) em (2), vem:
2.g.y = 6.g.x => 6.x = 2.y => 3x = y (3)
x + y = h => x + 3.x = h => 4x = h => x = h/4
Alternativa: D
16. (FEI-SP)
Da calçada, João atira para cima uma pequena esfera de vidro com
velocidade de 20 m/s. No mesmo instante, Pedro solta uma esfera igual de uma altura de 50 m acima do ponto de lançamento. Em que altura acima do ponto de lançamento as duas esferas se encontraram pela 1ª vez?
A) 18,75 m
B) 32,25 m
C) 25,00 m
D) 30,00 m
E) 15,25 m
Resolução:
Orientando-se a trajetória para cima e considerando o solo como origem dos espaços podemos escrever as funções horárias das esferas.
Esfera que desce:
Sd = 50 - 5.t2
Esfera que sobe:
Ss = 20.t - 5.t2
No instante do encontro:
Sd = Ss => 50 - 5.t2 = 20.t - 5.t2 => 20.t = 50 => t = 2,5 s
Substituindo-se t = 2,5 s na função horária Ss obtemos a altura H do encontro:
H = 20.(2,5)- 5.(2,5)2 => H = 50 - 31,25 => H = 18,75 m
Alternativa: A
17. (FUVEST-SP)
Orientando-se a trajetória para cima e considerando o solo como origem dos espaços podemos escrever as funções horárias das esferas.
Esfera que desce:
Sd = 50 - 5.t2
Esfera que sobe:
Ss = 20.t - 5.t2
No instante do encontro:
Sd = Ss => 50 - 5.t2 = 20.t - 5.t2 => 20.t = 50 => t = 2,5 s
Substituindo-se t = 2,5 s na função horária Ss obtemos a altura H do encontro:
H = 20.(2,5)- 5.(2,5)2 => H = 50 - 31,25 => H = 18,75 m
Alternativa: A
17. (FUVEST-SP)
Numa filmagem, no exato instante em que um caminhão passa por uma marca no chão, um dublê se larga de um viaduto para cair dentro de sua caçamba. A velocidade v do caminhão é constante e o dublê inicia sua queda a partir do repouso, de uma altura de 5 m da caçamba, que tem 6 m de comprimento. A velocidade ideal do caminhão é aquela em que o dublê cai bem no centro da caçamba, mas a velocidade real v do caminhão poderá ser diferente e ele cairá mais à frente ou mais atrás do centro da caçamba. Para que o dublê caia dentro da caçamba, v pode diferir da velocidade ideal, em módulo, no máximo: (g = 10 m/s2)
A) 1 m/s.
B) 3 m/s.
C) 5 m/s.
D) 7 m/s.
E) 9 m/s.
Resolução:
Tempo de queda do dublê:
H = 5.(tq)2 => 5 = 5.(tq)2 => (tq)2 = 1 => tq = 1 s
Velocidade do caminhão para que o dublê caia no meio da caçamba:
v = Δs/Δt => v = 3/1 m/s => v = 3 m/s
Velocidade limite do caminhão para que o dublê caia na extremidade final da caçamba:
vL = Δs/Δt => vL = 6/1 => vL = 6 m/s
Diferença das velocidades: vL - v = (6 m/s - 3 m/s) = 3 m/s
Alternativa: B
18. (UFV-MG)
Tempo de queda do dublê:
H = 5.(tq)2 => 5 = 5.(tq)2 => (tq)2 = 1 => tq = 1 s
Velocidade do caminhão para que o dublê caia no meio da caçamba:
v = Δs/Δt => v = 3/1 m/s => v = 3 m/s
Velocidade limite do caminhão para que o dublê caia na extremidade final da caçamba:
vL = Δs/Δt => vL = 6/1 => vL = 6 m/s
Diferença das velocidades: vL - v = (6 m/s - 3 m/s) = 3 m/s
Alternativa: B
18. (UFV-MG)
Uma bola e lançada horizontalmente com velocidade inicial v0. Ao percorrer horizontalmente 30 m ela cai verticalmente 20 m, conforme0mostrado no gráfico ao lado. Considere0a aceleração da gravidade igual a 10 m/s2 e despreze a resistência do ar.
É correto afirmar que o módulo da velocidade de lançamento v0 é:
A) 15 m/s
B) 30 m/s
C) 7,5 m/s
D) 60 m/s
Resolução:
Tempo de queda:
H = 5.(tq)2 => 20 = 5.(tq)2 => (tq)2 = 4 => tq = 2 s
Velocidade horizontal (constante):
v = Δs/Δt => v = 30/2 => v = 15 m/s
Alternativa: A
19. (FEI-SP)
Tempo de queda:
H = 5.(tq)2 => 20 = 5.(tq)2 => (tq)2 = 4 => tq = 2 s
Velocidade horizontal (constante):
v = Δs/Δt => v = 30/2 => v = 15 m/s
Alternativa: A
19. (FEI-SP)
Em que ângulos, em relação à horizontal, devemos posicionar um canhão para obter a altura máxima e o alcance máximo da trajetória do projétil, respectivamente? Despreze a resistência do ar.
A) 45º e 90º
B) 45º e 60º
C) 60º e 45º
D) 45º e 45º
E) 90º e 45º
Resolução:
A altura é máxima quando a componente vertical da velocidade inicial (v0y) é máxima.
v0y = v0.sen θ => v0y é máxima quando sen θ = 1 => θ = 90º.
Alcance: A = vx.t => t = ttotal = 2.ts => ts = tempo de subida.
t = ts quando vy = 0 => vy = v0.sen θ - g.ts => 0 = v0.sen θ - g.ts =>
ts = (v0.sen θ)/g
A = vx. 2.(v0.sen θ)/g => A = v0.cos θ.2.(v0.sen θ)/g =>
A = [(v0)2.2.sen θ.cos θ]/g => A = [(v0)2.sen 2θ]/g
A é máximo quando sen 2θ = 1 => 2θ = 90º => θ = 45º.
Alternativa: E
20. (UFPB)
A altura é máxima quando a componente vertical da velocidade inicial (v0y) é máxima.
v0y = v0.sen θ => v0y é máxima quando sen θ = 1 => θ = 90º.
Alcance: A = vx.t => t = ttotal = 2.ts => ts = tempo de subida.
t = ts quando vy = 0 => vy = v0.sen θ - g.ts => 0 = v0.sen θ - g.ts =>
ts = (v0.sen θ)/g
A = vx. 2.(v0.sen θ)/g => A = v0.cos θ.2.(v0.sen θ)/g =>
A = [(v0)2.2.sen θ.cos θ]/g => A = [(v0)2.sen 2θ]/g
A é máximo quando sen 2θ = 1 => 2θ = 90º => θ = 45º.
Alternativa: E
20. (UFPB)
Em uma partida de futebol, o goleiro bate um tiro de meta com a bola no nível do gramado. Tal chute dá à bola uma velocidade inicial de módulo 20 m/s e um ângulo de lançamento de 45º. Nessas condições, a distância mínima que um jogador deve estar do ponto de lançamento da bola, para recebê-la no seu primeiro contato com o solo, é:
(g = 10 m/s2; sen 45º = cos 45º = √2/2)
(g = 10 m/s2; sen 45º = cos 45º = √2/2)
A) 30m
B) 40m
C) 20m
D) 10m
E) 5m
Resolução:
O alcance é dado pela fórmula:
A = [(v0)2.sen 2θ]/g => A = [(20)2. sen (90º)]/10 =>
A = (400.1)/10 => A = 40 m
Alternativa: B
Resolução:
O alcance é dado pela fórmula:
A = [(v0)2.sen 2θ]/g => A = [(20)2. sen (90º)]/10 =>
A = (400.1)/10 => A = 40 m
Alternativa: B
21. (UEA-AM)
Um garoto sentado no chão lança uma bolinha de gude na direção de um buraco situado a 2 metros de distância, em um terreno horizontal. A bolinha parte do solo em uma direção que faz um ângulo de 45º acima da horizontal. Despreze a resistência do ar. Para que a bolinha caia dentro do buraco, o módulo da velocidade inicial de lançamento, em m/s, deve ser
A) √10 xxxxxxxxxxxxxDados: g = 10 m/s2
B) √20 xxxxxxxxxxxxxsen 45º = cos 45º = √2/2
C) √30
D) √40
E) √50
Resolução:
Cálculo do tempo de subida tS
t = tS quando v0 = 0
vy = v0y - g.t => 0 = v0.sen 45º - 10.tS => tS = v0.√2/20
Cálculo do tempo total ttotal
ttotal = 2.tS = v0.√2/10
Cálculo de v0
x = A = 2 m, quando t = ttotal
x = vx.t => 2 = v0.√2/2.v0.√2/10 => v0 = √20 m/s
Alternativa: B
22. (UFPR)
Cálculo do tempo de subida tS
t = tS quando v0 = 0
vy = v0y - g.t => 0 = v0.sen 45º - 10.tS => tS = v0.√2/20
Cálculo do tempo total ttotal
ttotal = 2.tS = v0.√2/10
Cálculo de v0
x = A = 2 m, quando t = ttotal
x = vx.t => 2 = v0.√2/2.v0.√2/10 => v0 = √20 m/s
Alternativa: B
22. (UFPR)
A figura abaixo mostra um modelo de uma catapulta no instante em que o seu braço trava e o objeto que ele carrega é arremessado, isto é, esse objeto se solta da catapulta (a figura é meramente ilustrativa e não está desenhada em escala). No instante do lançamento, o objeto está a uma altura de 1,0 m acima do solo e sua velocidade inicial V0 forma um ângulo α de 45º em relação à horizontal. Suponha que a resistência do ar e os efeitos do vento sejam desprezíveis. Considere a aceleração da gravidade como sendo de 10 m/s2. No lançamento, o objeto foi arremessado a uma distância de 19 m, medidos sobre o solo a partir do ponto em que foi solto. Assinale a alternativa que contém a estimativa correta para o módulo da velocidade inicial do objeto.
sen 45º = cos 45º = √2/2
A) Entre 13,4 m/s e 13,6 m/s.
B) Entre 12 m/s e 13 m/s.
C) Menor que 12 m/s.
D) Entre 13,6 m/s e 13,8 m/s.
E) Maior que 13,8 m/s.
Resolução:
Ao atingir o solo, temos y = 0 e x = 19 m
x = vx.t => 19 = v0.(√2/2).t => t = 19√2/v0
y = 1,0 + v0y.t - g.t2/2 => y = 1,0 + v0.(√2/2).t - 5.t2 =>
0 = 1,0 + 19 - 5.(19√2/v0)2 => 20 = 5.(361.2)/v02
v0 ≈ 13,43 m/s
Alternativa: B
23. (AFA-SP)
Ao atingir o solo, temos y = 0 e x = 19 m
x = vx.t => 19 = v0.(√2/2).t => t = 19√2/v0
y = 1,0 + v0y.t - g.t2/2 => y = 1,0 + v0.(√2/2).t - 5.t2 =>
0 = 1,0 + 19 - 5.(19√2/v0)2 => 20 = 5.(361.2)/v02
v0 ≈ 13,43 m/s
Alternativa: B
23. (AFA-SP)
No instante t = 0, uma partícula A é lançada obliquamente, a partir do solo, com velocidade de
80 m/s sob um ângulo de 30º com a horizontal. No instante t = 2 s, outra partícula B é lançada verticalmente para cima, também a partir do solo, com velocidade de 70 m/s, de um ponto situado a 200√3 m da posição de lançamento da primeira. Sabendo-se que essas duas partículas colidem no ar, pode-se afirmar que no momento do encontro.
(Dado: sen 30º = 1/2; cos 30º = √3/2)
80 m/s sob um ângulo de 30º com a horizontal. No instante t = 2 s, outra partícula B é lançada verticalmente para cima, também a partir do solo, com velocidade de 70 m/s, de um ponto situado a 200√3 m da posição de lançamento da primeira. Sabendo-se que essas duas partículas colidem no ar, pode-se afirmar que no momento do encontro.
(Dado: sen 30º = 1/2; cos 30º = √3/2)
A) ambas estão subindo.
B) A está subindo e B descendo.
C) B está subindo e A descendo.
D) ambas estão descendo.
Resolução:
Partícula A
x = vx.t => 200.√3 = (80.√3/2).t => t = 5 s
vAy = v0y - g.t => vAy = 80.1/2 - 10.5 =>
vAy = -10 m/s < 0 => descendo
Partícula B
vB = v0B - g(t-2) => vB = 70 - 10.(5-2) =>
vB = 40 m/s > 0 => subindo
Alternativa: C
24. (UESPI)
Partícula A
x = vx.t => 200.√3 = (80.√3/2).t => t = 5 s
vAy = v0y - g.t => vAy = 80.1/2 - 10.5 =>
vAy = -10 m/s < 0 => descendo
Partícula B
vB = v0B - g(t-2) => vB = 70 - 10.(5-2) =>
vB = 40 m/s > 0 => subindo
Alternativa: C
24. (UESPI)
Considere a situação em que um corpo descreve um movimento circular uniforme. Para cada instante deste movimento, podemos dizer que os vetores velocidade e aceleração formam entre si um ângulo
de:
A) 0º
B) 30º
C) 45º
D) 90º
E) 180º
Resolução:
Como o corpo descreve um MCU sua aceleração é centrípeta e portanto perpendicular à velocidade vetorial em cada instante. Assim, os vetores velocidade e aceleração formam entre si um ângulo de 90º.
Alternativa: D
25. (UFV-MG)
Como o corpo descreve um MCU sua aceleração é centrípeta e portanto perpendicular à velocidade vetorial em cada instante. Assim, os vetores velocidade e aceleração formam entre si um ângulo de 90º.
Alternativa: D
25. (UFV-MG)
Uma pedra esta fixa na periferia de uma roda de raio R = 2 m e gira com velocidade linear de módulo constante V. Se A e o módulo da aceleração da pedra, das opções abaixo, aquela que apresenta valores para V e A, em acordo com a cinemática do movimento circular uniforme, e:
A) V = 2 m/s e A = 2 m/s2.
B) V = 1 m/s e A = 4 m/s2.
C) V = 4 m/s e A = 6 m/s2.
D) V = 6 m/s e A = 0 m/s2.
Resolução:
Sendo o movimento circular com velocidade linear V de módulo constante, concluímos que a aceleração A é centrípeta, valendo a relação: A = V2/R. Sendo R = 2 m, concluímos que das alternativas dadas a que obedece a fórmula da aceleração centrípeta é a alternativa A.
Alternativa: A
26. (UECE)
Sendo o movimento circular com velocidade linear V de módulo constante, concluímos que a aceleração A é centrípeta, valendo a relação: A = V2/R. Sendo R = 2 m, concluímos que das alternativas dadas a que obedece a fórmula da aceleração centrípeta é a alternativa A.
Alternativa: A
26. (UECE)
Dois corpos em movimento circular uniforme estão alinhados como mostra a figura. Sabendo-se que o raio da trajetória maior é o dobro do raio da trajetória menor, qual deve ser a razão de suas velocidades (vM/vm) para que eles ocupem a mesma posição mostrada na figura, quando o corpo M completar uma volta e o m completar quatro voltas?
A) 2
B) 1
C) 1/2
D) 1/4
Resolução:
Corpo M
2π.R = vM.t (1)
Corpo m
4.2π.R/2 = vm.t (2)
Dividindo membro a membro (1) por (2), temos: vM/vm = 1/2
Alternativa: C
27. (UEMS)
Corpo M
2π.R = vM.t (1)
Corpo m
4.2π.R/2 = vm.t (2)
Dividindo membro a membro (1) por (2), temos: vM/vm = 1/2
Alternativa: C
27. (UEMS)
A figura mostra a polia A, de raio RA = 10 cm, ligada à polia B, de raio RB = 5 cm, por uma correia que não desliza enquanto gira.
Baseando- se nesses direcionamentos, analise as afirmativas:
I. A velocidade tangencial da polia A é exatamente igual a metade da velocidade tangencial da polia B.
II. Se o período da polia A for igual a 1 s, o período da polia B será 0,5 s.
III. A velocidade angular da polia A (ωA) é igual a velocidade angular da polia B (ωB).
Assinale a alternativa que apresenta a(s) afirmativa(s) correta(s):
A) I
B) II
C) III
D) I e III
E) I, II e III
Resolução:
I) Incorreta. Como não há deslizamento as velocidades tangenciais de A e B são iguais: vA = vB
II) Correta: De vA = vB, vem:
ωA.RA = ωB.RB
fA.RA = fB.RB
RA/TA = RB/TB => 10/1 = 5/TB => TB = 0,5 s
III) Incorreta: RA ≠ RB => ωA ≠ ωB
Alternativa: B
28. (UNIOEST-PR)
A polia A de raio 10 cm esta acoplada à polia B de raio 36 cm por uma correia, conforme mostra a figura.
I) Incorreta. Como não há deslizamento as velocidades tangenciais de A e B são iguais: vA = vB
II) Correta: De vA = vB, vem:
ωA.RA = ωB.RB
fA.RA = fB.RB
RA/TA = RB/TB => 10/1 = 5/TB => TB = 0,5 s
III) Incorreta: RA ≠ RB => ωA ≠ ωB
Alternativa: B
28. (UNIOEST-PR)
A polia A de raio 10 cm esta acoplada à polia B de raio 36 cm por uma correia, conforme mostra a figura.
A polia A parte do repouso e aumenta uniformemente sua velocidade angular à razão de
3,14 rad/s2. Supondo que a correia não deslize e que a polia B parte do repouso, o tempo necessário para a polia B alcançar a frequência de 100 rpm será de
A) 1,91 s
B) 3,82 s
C) 12,00 s
D) 3,00 s
E) 3,60 s
3,14 rad/s2. Supondo que a correia não deslize e que a polia B parte do repouso, o tempo necessário para a polia B alcançar a frequência de 100 rpm será de
A) 1,91 s
B) 3,82 s
C) 12,00 s
D) 3,00 s
E) 3,60 s
Resolução:
ωA.RA = ωB.RB => γ.t.RA = 2π.fB.RB => π.t.10 = 2π.(100/60).36 =>
t = 12 s
Alternativa: C
29. (UEPA)
O nascimento da automação industrial se deu em 1788 com o dispositivo mostrado na figura abaixo, conhecido como regulador de Watt, em homenagem ao seu inventor. Esse dispositivo era usado nas máquinas a vapor, para regular automaticamente a abertura de válvulas e assim controlar o fluxo de vapor em função da velocidade de rotação da máquina. Se, na situação mostrada, as massas se movem em um plano horizontal, com velocidade linear constante em módulo, executando 120 rpm, então:
A) ambas têm a mesma frequência de 0,5 Hz.
B) ambas possuem velocidades angulares diferentes.
C) o módulo da velocidade linear v não depende do raio da trajetória R.
ωA.RA = ωB.RB => γ.t.RA = 2π.fB.RB => π.t.10 = 2π.(100/60).36 =>
t = 12 s
Alternativa: C
29. (UEPA)
O nascimento da automação industrial se deu em 1788 com o dispositivo mostrado na figura abaixo, conhecido como regulador de Watt, em homenagem ao seu inventor. Esse dispositivo era usado nas máquinas a vapor, para regular automaticamente a abertura de válvulas e assim controlar o fluxo de vapor em função da velocidade de rotação da máquina. Se, na situação mostrada, as massas se movem em um plano horizontal, com velocidade linear constante em módulo, executando 120 rpm, então:
A) ambas têm a mesma frequência de 0,5 Hz.
B) ambas possuem velocidades angulares diferentes.
C) o módulo da velocidade linear v não depende do raio da trajetória R.
D) suas acelerações não são nulas.
E) executam uma volta completa em 2 s.Resolução:
A) Errada. Ambas têm a mesma frequência igual a 120/60 Hz = 2 Hz
B) Errada. As velocidades angulares são iguais.
C) Errada. V depende de R: v = ω.R
D) Correta. Suas acelerações são centrípetas
E) Errada. Executam uma volta completa em um período T = 1/f = 0,5 s.
Alternativa: D
30. (UFT-TO)
Em um relógio analógico comum existem três ponteiros: o ponteiro das horas, o dos minutos e o dos segundos. A ponta de cada um desses ponteiros descreve um movimento circular uniforme. Se a ponta do ponteiro dos segundos possui módulo da velocidade igual a 6 cm/s, qual é o valor que melhor representa o diâmetro da trajetória circular percorrida pela ponta deste ponteiro?
A) 1,15 m
B) 1,71 m
C) 0,57 m
D) 0,81 m
E) 2,10 m
Resolução:
v = ω.R => v = (2π/T).R =. 6 = (2.R/60).3,14 =>
2.R = diâmetro = 6.60/3,14 (cm) ≈ 1,15 m
Alternativa: A





















Eu gostaria de saber o porque que na questão 4. (fuvest) a gente divide e na questão 6. (ufcg-pb) a gente multiplica ?
ResponderExcluir