Caiu no vestibular

Hoje e na próxima semana o tema desta seção do blog será a Estática. Continue conosco. Mais questões virão, cada uma mais interessante do que a outra.

Exercício 1:

(Famerp) Um vaso de flores de massa total igual a 4,8 kg está pendurado, em equilíbrio, em um suporte preso a uma parede vertical. O suporte está pendurado em um parafuso preso ao ponto A e apoiado na parede no ponto B, conforme representado na figura.

Considere g = 10 m/s² e que a massa do suporte seja desprezível. O módulo da força horizontal exercida pelo suporte na parede, no ponto B, é igual a

a) 60 N.        b) 80 N.        c) 20 N.        d) 40 N.        e) 100 N.

Resolução:

Vamos representar as forças que agem no suporte:

Soma dos momentos nula em relação ao ponto A:

P.50 – F.30 = 0
48.50 = F.30 => F = 80 N

Resposta: b

Exercício 2:

(Universidade Anhembi-Morumbi – Prova Medicina)
O peso (P) do tampo de uma mesa desmontável aplica-se sobre os pés de um cavalete que se mantém firme devido à ação das duas travas paralelas que se encontram sob o tampo.

O atrito dos pés do cavalete com o chão é desprezível e o cavalete se mantém aberto sob o ângulo indicado na figura. Quando a mesa está montada e nada se apoia sobre ela, além do tampo, a intensidade da componente horizontal da força (Fh) que uma das travas da mesa suporta é dada pela expressão:

(A) Fh = P x sen2θ
(B) Fh = P x tgθ
(C) Fh = P/2 x tgθ/2
(D) Fh = P x tgθ/2
(E) Fh = P/2 x senθ/2

Resolução:

Sendo P o peso do tampo, concluímos que o chão exerce em cada pé do cavalete uma força de intensidade P/4. Assim, em cada uma das quatro hastes do cavalete, temos as forças:

Soma dos momentos nula em relação ao ponto O:

(P/4). L sen (θ/2) +(P/4). L sen (θ/2) – Fh. L cos (θ/2) = 0
2. (P/4). L sen (θ/2) = Fh. L cos (θ/2)
Fh = (P/2). tg (θ/2)

Resposta: (C)

Exercício 3:

(Fema-Prova Medicina)Em uma exposição, um quadro homogêneo de peso 240 N deve ser preso ao teto por dois fios idênticos que formam um ângulo θ com a vertical, como mostra a figura.

Se os fios suportam, sem romper, uma tração máxima de 160 N cada um, o máximo valor que o ângulo θ pode assumir nessa situação é tal que

(A) sen θ = 0,50.
(B) sen θ = 0,75.
(C) sen θ = 0,25.
(D) cos θ = 0,25.
(E) cos θ = 0,75.

Resolução:

Forças que agem no quadro:

Equilíbrio na direção vertical:

T.cos θ + T.cos θ = P => 2.160.cos θ = 240 => cos θ = 240/320 = 0,75

Resposta: (E)

Exercício 4:

(UEA)
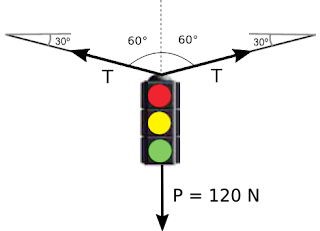
Um semáforo de peso 120 N é sustentado por dois cabos que formam ângulos de 30° com a horizontal, como indicado na figura.

Sendo sen 30° = 0,50 e cos 30° = 0,87, é correto afirmar que a tração em cada um dos cabos vale

(A) 104 N.
(B) 120 N.
(C) 87 N.
(D) 60 N.
(E) 30 N.

Resolução: 

Forças que agem no semáforo:

Equilíbrio na direção vertical:

T.cos 60° + T.cos 60° = P => 2.T.0,50 = 120 => T = 120 N

Resposta: (B)