Seção nova

Sobre o Desafio de Mestre Especial

Hoje iniciamos uma nova seção no Blog com exercícios especialmente selecionados para ajudar os estudantes de nível médio a enfrentar desafios.

Os exercícios terão orientação para a resolução e darão um prêmio (livro) ao primeiro leitor que apresentar a solução correta.

Posto isto, leia atentamente o enunciado do exercício abaixo, siga as instruções e ganhe o prêmio.

Boa sorte.

Borges e Nicolau

Desafio de Mestre (Especial)

Clique para ampliar

Bloco num plano inclinado

x

Borges e Nicolau

Um bloco homogêneo de peso P = 10 N está apoiado num plano inclinado de um ângulo α tal que: senα = 0,6 e cosα = 0,8. A seção transversal do bloco é um quadrado de lado a. O coeficiente de atrito estático entre o bloco e o plano é μ = 0,5. Qual é o valor máximo da intensidade F da força horizontal, aplicada em B, de modo que o bloco não escorregue para cima e nem tombe em torno de A?

Orientação para a resolução:

• Decomponha o peso P do bloco nas componentes:
Pt = Psenα e Pn = Pcosα.

• Decomponha a força F numa componente paralela ao plano inclinado (Fcosα) e numa componente perpendicular ao plano inclinado (Fsenα).

• Represente a força de atrito, considerando que o bloco tende a escorregar para cima. O valor máximo de F corresponde à iminência de subir. Neste caso, Fat = μFN. Imponha resultante nula.

• Ao estudar o tombamento, considere que o máximo valor de F corresponde ao bloco na iminência de tombar em torno de A. Nestas condições, a força normal FN passa pelo ponto A. Imponha soma algébrica dos momentos nula, em relação ao ponto A.

Sábado (04/09) apresentaremos a solução.

Sensação térmica

O grau de umidade do ar *

Paulo de Toledo Soares
A sensação de calor está intimamente ligada ao grau de umidade do ar. O limite ideal está entre 50% e 70% para o grau higrométrico. Nesta faixa, há uma evaporação eficiente do suor, de modo que a perda de calor pelo organismo que consegue manter constante sua temperatura corporal.

Quando a umidade é alta, mesmo que a temperatura ambiente não chegue a alcançar valor muito elevado, a sensação de calor é sufocante e opressiva: a velocidade de evaporação do suor é reduzida, devido à grande quantidade de vapor existente na atmosfera.

Entretanto, quando a umidade relativa é muito baixa, há conseqüências ainda mais graves, não só para a população como também para o ambiente. Para as pessoas, há o ressecamento das mucosas que levam a complicações respiratórias, sangramento nasal, ressecamento da pele, irritação dos olhos, etc. Estes sintomas se intensificam com a poluição atmosférica e com o grau de debilidade do indivíduo, sobretudo no caso de crianças e idosos.

Pessoas com problemas reumáticos e respiratórios preexistentes podem ter seu quadro clínico agravado. No ambiente, o ar seco produz eletricidade estática que pode danificar equipamentos eletrônicos. Além disso, aumenta consideravelmente a possibilidade de incêndios em pastagens e florestas.

Segundo normas da Defesa Civil de vários estados e da Cetesb (agência ambiental paulista), caso a umidade relativa caia abaixo de 30%, são estabelecidos os estados de atenção, alerta e emergência, de acordo com os valores medidos. Nessas situações, há uma série de procedimentos a serem tomados pela população, apresentados no quadro abaixo.

Portanto, é de grande importância a medida do grau higrométrico do ar. Esta informação sempre está incluída nos boletins meteorológicos. Essa avaliação é feita por meio de aparelhos denominados higrômetros.

· Entre 20 e 30%
- Estado de atenção Evitar exercícios físicos ao ar livre entre 11 e 15 horas. Umidificar o ambiente utilizando vaporizadores, toalhas molhadas, recipientes com água, etc. Sempre que possível permanecer em locais protegidos do sol, preferencialmente em áreas verdes. Ingerir líquidos, para evitar desidratação.

· Entre 12 e 20%
- Estado de alerta Além das recomendações do estado de atenção, devem ser suprimidos os exercícios físicos e trabalhos ao ar livre entre 10 e 16 horas. Aglomerações em ambientes fechados devem ser evitadas. É recomendável o uso de soro fisiológico para os olhos e as narinas.

· Abaixo de 12%
- Estado de emergência Além das recomendações estabelecidas para os estados de atenção e de alerta, é determinante a interrupção de qualquer atividade ao ar livre entre 10 e 16 horas, como aulas de educação física, coleta de lixo, entrega de correspondência, etc. Devem ser suspensas quaisquer atividades que exijam aglomerações de pessoas em recintos fechados como aulas, sessões de cinema e teatro, etc. entre 10 e 16 horas. Os ambientes internos devem ser mantidos continuamente umidificados, principalmente quartos de crianças e de doentes, seja em casa ou em hospitais.

* Publicado no Blog em 18 / 06 / 2009.

Arte do Blog

Clique para ampliar

Meninos com cordeiro

Borges e Nicolau
No quadro de Cândido Portinari há um menino plantando bananeira, brincadeira comum na infância, mas que requer habilidade.

O menino retratado está apoiado apenas em uma das mãos, posição que necessita um posicionamento preciso do centro de gravidade do corpo, situado aproximadamente ao redor do umbigo.

Para que o equilíbrio seja mantido a reta vertical que contém o centro de gravidade deve passar pela base de apoio, no caso a mão espalmada. A parte sombreada mostra o campo de variação do centro de gravidade.

Candido Portinari tinha grande apreço pelo Brasil e pelos problemas sociais do país e isso ficou retratado em sua obra. Mas também tinha uma visão doce e poética da infância, das brincadeiras e das festas populares que tanto marcam a vida dos brasileiros.

Saiba mais sobre Cândido Portinari aqui.

Leituras do Blog

O ano-luz

Os astrônomos, tendo em vista a ordem de grandeza das distâncias entre os astros no universo, criaram uma unidade maior que as usuais (metro e quilômetro) para medi-las: o ano-luz. Para isso, basearam-se na velocidade da luz no vácuo.

Ano-luz é a distância que a luz percorre no vácuo em um ano.

Para se ter uma idéia de quanto é grande essa unidade, basta dizer que ela corresponde a quase 10 trilhões de quilômetros, isto é, 10.000.000.000.000 de quilômetros.

Assim, quando dizemos que uma estrela está, por exemplo, a 400 mil anos-luz da Terra, significa que a luz desta estrela leva 400 mil anos para chegar até nós.

Então, ao admirarmos o céu estrelado, estaremos na verdade olhando para o passado, pois a luz que estamos recebendo abandonou a fonte há milhares e milhares de anos. Quantos daqueles astros que observamos já estarão extintos, embora ainda presentes no firmamento?
(Do livro “ O Mundo da Cores” de Paulo Toledo Soares)

Saiba mais. Clique aqui

Pense & Responda

Questão 1. (ENEM)

SEU OLHAR

(Gilberto Gil)

Veja o clip aqui

Na eternidade
Eu quisera ter
Tantos anos-luz
Quantos fosse precisar
Pra cruzar o túnel
Do tempo do seu olhar

Gilberto Gil usa na letra da música a palavra composta anos-luz. O sentido prático, em geral, não é obrigatoriamente o mesmo que na ciência. Na Física, um ano luz é uma medida que relaciona a velocidade da luz e o tempo de um ano e que, portanto, se refere a:

(A) tempo.

(B) aceleração.

(C) distância.

(D) velocidade.

(E) luminosidade.


Questão 2. (Fuvest-SP)

Uma estrela emite radiação que percorre a distância de 1 bilhão de anos-luz, até chegar à Terra e ser captada por um telescópio. Isto quer dizer que:

(A) A estrela está a 1 bilhão de quilômetros da Terra.

(B) Daqui a 1 bilhão de anos, a radiação da estrela não será mais observada na Terra.

(C) A radiação recebida hoje na Terra foi emitida pela estrela a 1 bilhão de anos.

(D) Hoje, a estrela está a 1 bilhão de anos- luz da Terra.

(E) Quando a radiação foi emitida pela estrela, ela tinha a idade de 1 bilhão de anos.

Respostas da semana

Pense & Responda de 23/08

1) Afastando-se o espelho esférico do rosto a imagem diminui de tamanho, é sempre direita e afasta-se do espelho. 2) A imagem de L localiza-se no ponto B.

Clique para ampliar

Pense & Responda de 24/08

1) No farol o filamento da lâmpada L deve ser colocado no foco principal F. Assim, o feixe refletido é de raios paralelos.

Clique para ampliar

2) O espelho deve ser côncavo. Voltando-se o espelho para o Sol, os raios de luz incidentes, que são praticamente paralelos, refletem convergindo para o foco principal F. Neste ponto há maior concentração de energia. Portanto, o pedacinho de papel deve ser colocado no foco principal F.

Clique para ampliar

3) Se a imagem virtual e direita é menor do que o objeto, o espelho é convexo. Sendo maior, é côncavo.

4) A imagem de um objeto colocado sobre o centro de curvatura C forma-se no próprio centro de curvatura C. A imagem de um objeto no foco forma-se no infinito. Portanto, ao se deslocar um objeto do centro de curvatura C ao foco principal F, a imagem se desloca de C ao infinito. Alternativa b.

Desafio de mestre

Cadê a imagem

Clique para ampliar

Pense & Responda de 25/08

1) Estando a esfera em equilíbrio, vem:

P = E = > DVg = > d/D = V/v

2) A relação independe da aceleração da gravidade. Logo, é a mesma na Terra e na Lua.

3) Nesta caso, v = V. Portanto: d/D = 1 = > d = D

4) P = EA e P = EB. Portanto: EA = EB = > dAVA = dBVB.

Sendo VA menor do que VB, resulta dA maior do que dB.

5) O peso da esfera é igual ao peso do líquido que extravasa. Como esta parte do líquido é retirada, a indicação da balança não se altera:

P2 = 10 N

Desafio de mestre

A força que a água exerce no cilindro A é o empuxo e tem intensidade

E = 1N

De E = dágua . Vimerso . g, vem:

1 = 1,0 . VA . 10

VA = 0,1 L

VA = 0,1 . 1000 cm³

VA = 100 cm³

Resposta: C

Óptica geométrica

Clique para ampliar

x

Luz incidente em espelhos esféricos

Casos particulares

Borges e Nicolau

Quando o raio de luz incide em uma direção qualquer, o raio refletido passa por um foco secundário F' que está na intersecção do eixo secundário com o plano focal. O eixo secundário é paralelo ao raio de luz incidente, passando pelo centro de curvatura C do espelho. O plano focal é perpendicular ao eixo principal e passa pelo foco principal F.

Desafio de Mestre

Clique para ampliar

Espelho convexo

x

Borges e Nicolau

Num espelho esférico convexo de vértice V, foco principal F e centro de curvatura C, incidem os raios r e s, conforme indica figura. Refaça o esquema dado numa folha de papel e desenhe os correspondentes raios refletidos.

Cientistas do Blog

Arquimedes de Siracusa
Pintura de Domenico Fetti (1620)

x

Arquimedes de Siracusa

x

Borges e Nicolau

Arquimedes nasceu em Siracusa, na Sicília em 287 aC e morreu também em Siracusa, em 212 aC. Siracusa pertencia à região chamada Magna Grécia. Realizou seus estudos em Alexandria e deixou para a humanidade inúmeras invenções e descobertas. Seu pai, Fídias, era astrônomo, passando à história por ser o pai de Arquimedes, mas certamente contribuiu para despertar a curiosidade daquele que viria a ser um dos maiores desvendadores dos segredos naturais de todos os tempos. Em certa fase da vida Arquimedes visitou o Egito, onde inventou um sistema capaz de transportar água a pontos mais elevados, chamado Parafuso de Arquimedes, ainda utilizado nos dias atuais.

xAo contemplar o tratado de Estática de Arquimedes, que abrangia desde os princípios fundamentais relativos ao centro de gravidade até às alavancas, o rei Hierão, de Siracusa, teria dito: "Acharei de hoje em diante possível tudo quanto me disser Arquimedes!"

x

Tal afirmativa, partindo do rei, fez com que Arquimedes replicasse: "Dêem-me um ponto de apoio e, com a minha alavanca, erguerei o mundo".

Gravura alusiva à afirmação de Arquimedes

Para continuar a maravilhar o rei, Arquimedes movimentou um navio carregado com sua força muscular, que não era grande, multiplicada por um sistema de polias, conhecido como talha, amplamente utilizado até hoje.

xTambém é atribuido a Arquimedes o uso de espelhos côncavos para incendiar as velas dos navios romanos invasores. Tal fato é possível, mas pouco provável em face aos recursos tecnológicos da época. Os espelhos eram de bronze, sendo seu polimento feito com areia.

x

Por falar em lendas, a mais famosa em relação ao sábio e relatada pelo arquiteto romano Vitrúvio, no século I dC, diz que o rei Hierão mandou fazer uma coroa de ouro. Como a coroa não brilhasse como era esperado e dando ouvidos aos boatos de que o ourives teria usado menos ouro do que o rei pedira, Hierão convocou Arquimedes que já era um famoso filósofo, como eram conhecidos estudiosos e cientistas.

x

Consultado sobre a composição da coroa, Arquimedes foi pensar na banheira. Dizem que ele costumava passar horas entretido com questões filosóficas mergulhado em água morna e sais de banho. Ao ver a água transbordar quando entrou na banheira, Arquimedes teve um momento de inspiração e vislumbrou a solução do problema. Entusiasmado, saiu correndo, nu pelas ruas de Siracusa, gritando “Eureka, Eureka!”, que em grego quer dizer “Descobri, descobri!”.

x

Pois saibam que nesse instante nasceu o que hoje conhecemos como "Princípio de Arquimedes" (referente à força que age sobre qualquer corpo mergulhado num líquido: o empuxo).

x

Arquimedes mergulhou a coroa num recipiente completamente cheio de água e mediu o volume derramado. A seguir, mergulhou blocos de ouro e prata com pesos iguais ao da coroa e mediu as quantidades que transbordaram. O volume transbordado pela coroa ficou entre os volumes derramados pelos blocos de ouro e prata, provando que o ourives não tinha sido honesto.

x

Arquimedes foi coberto de glória pelo seu feito. Não vamos falar do triste destino do ourives. Não vale a pena.

x

Galileu Galilei, contestou essa versão, sugerindo que Arquimedes teria solucionado o problema usando uma balança hidrostática.

xSiga os links:

Para saber mais. (aqui)

x

Os mitos dos cientistas e suas controvérsias, de Rodrigo Moura e João Batista Garcia Canalle, Revista Brasileira de Ensino de Física, vol. 23, no 2, Junho, 2001. (aqui)

Empuxo

A balança acima foi projetada especialmente para a experiência que vamos realizar.

No prato do lado esquerdo colocamos um recipiente cheio de água e no prato do lado direito um peso de metal. O sistema está em equilíbrio.

Em seguida colocamos um corpo esférico no recipiente com água. Parte da água tranborda e é recolhida. O sistema já não está em equilíbrio, o peso do corpo esférico faz com que o lado esquerdo da balança, mais pesado, desça.

Colocando-se a água que transbordou no prato do lado direito, o sistema volta a ficar em equilíbrio. Podemos então concluir que o peso do volume de água deslocado pela presença do corpo esférico é igual ao peso do corpo esférico.

Isolando-se o corpo colocado na água, em equilíbrio, verificamos duas interações. Uma de campo, o peso P e outra de contato, aplicada pela água, denominada empuxo E. O empuxo E tem a mesma direção de P, mesma intensidade e sentido oposto ao de P. A intensidade do empuxo é igual ao peso do corpo esférico que é igual ao peso do volume de água deslocado.

P = E

E = mD . g

onde mD é a massa de água deslocada.

Esta conclusão é válida de um modo geral para corpos imersos em fluidos (líquidos ou gases):

E = dF.vD.g

Onde:

dF = densidade do fluido onde o corpo foi introduzido.

vD = volume de fluido deslocado (corresponde ao volume imerso do corpo).

g = aceleração da gravidade local.

Sendo dC a densidade do corpo e VC o volume do corpo, temos:

P = dC.VC.g

Pense & Responda

Hidrostática

Borges e Nicolau

Questão 1
Uma esfera de volume V, constituída de um material de densidade D, flutua parcialmente imersa num líquido de densidade d. Seja v a parte do volume da esfera que está imersa no líquido. Determine a relação d/D em função de v e V.


Questão 2
Retome a questão anterior. Se o sistema fosse levado à Lua onde a aceleração da gravidade é seis vezes menor do que a aceleração da gravidade na Terra, qual seria a relação d/D?


Questão 3
Retome a questão 2. Qual seria a relação d/D se a esfera estivesse em equilíbrio totalmente imersa no líquido e sem tocar o fundo do recipiente?


Questão 4
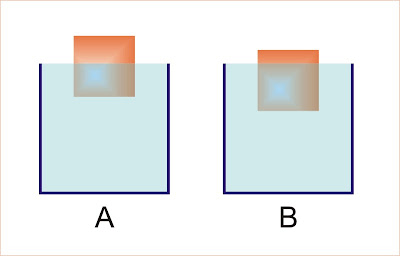
Dois cubos idênticos flutuam em líquidos A e B, conforme indica a figura. Qual dos líquidos tem maior densidade?

Questão 5
Um recipiente completamente cheio de água é colocado sobre uma balança que registra o valor 10 N ( figura a ). Uma esfera de peso 2 N é colocada na água e passa a flutuar parcialmente imersa( figura b). O volume de água extravasado é recolhido, sendo afastado do recipiente. Qual é a leitura da balança nesta nova situação?

Clique para ampliar

Desafio de Mestre

International Junior Science Olympiad (IJSO)

Dois cilindros, A sólido e fechado e B aberto em sua parte superior, cuja parte vazia tem o mesmo volume de A, são pendurados num dinamômetro conforme indica o esquema a. Nestas condições, o dinamômetro registra 3N. O cilindro A é imerso num recipiente contendo água e o dinamômetro passa a indicar 2N (esquema b).

Preenchendo-se o cilindro B com água, o dinamômetro volta a marcar 3N (esquema c). São dados a densidade da água, 1kg/L, e a aceleração da gravidade, 10m/s².

Pode-se afirmar que

a) a força que a água exerce no cilindro A tem intensidade 2N.

b) a força que a água exerce no cilindro A tem intensidade 3N.

c) o volume do cilindro A é de 100cm³.

d) o volume do cilindro A é de 200cm³.

e) Se a experiência fosse feita com mesmo material, mas utilizando-se álcool no lugar de água, os valores registrados pelo dinamômetro no esquema b seriam iguais.

Óptica geométrica

Clique nas imagens para ampliar

Lembrete: Espelho côncavo

x

Borges e Nicolau

Observe nas figuras objetos posicionados antes do centro de curvatura C, entre C e o foco principal F e entre F e o vértice V. As imagens fornecida pelo espelho côncavo são, respectivamente, real, invertida e menor; real invertida e maior; virtual, direita e maior.

Pense & Responda

Espelho côncavo

Borges e Nicolau

Questão 1
O farol de um carro é constituído essencialmente de um espelho esférico côncavo e de uma pequena lâmpada L. Sejam: V o vértice do espelho, F o foco principal e C o centro de curvatura do espelho.

Para que o farol funcione bem, onde deve ser colocado o filamento da lâmpada L? Em V, F ou C? Faça o esquema correspondente.


Questão 2
Um espelho esférico de vértice V, foco principal F e centro de curvatura C é utilizado para queimar um pequeno pedaço de papel, concentrando a luz solar. O espelho é côncavo ou convexo? Onde deve ser colocado o pedacinho de papel? Em V, F ou C? Faça o esquema correspondente.


Questão 3
A imagem de um objeto, formada por um espelho esférico, é virtual e direita. O espelho é côncavo ou convexo? Analise os casos:

• A imagem é menor do que o objeto

• A imagem é maior do que o objeto


Questão 4
Um objeto é deslocado do centro de curvatura C até o foco principal F de um espelho esférico côncavo. A correspondente imagem se desloca de:

a) F a C

b) C ao infinito

c) F até a superfície do espelho.

Qual é a alternativa está correta?

Desafio de Mestre

Cadê a imagem?

Borges e Nicolau
Um objeto retilíneo AB é colocado diante de um espelho esférico côncavo, paralelamente ao eixo principal, conforme indica a figura. C, F e V são, respectivamente, o centro de curvatura, o foco principal e o vértice do espelho. Refaça a figura numa folha de papel e obtenha a correspondente imagem A’B’.

Clique para ampliar

Óptica geométrica

Clique para ampliar

Lembrete: Espelho convexo

Borges e Nicolau
Observe que na figura os objetos se aproximam do espelho e suas respectivas imagens, situadas entre o foco e o vértice, também. Quanto mais afastado o objeto menor a imagem e mais próxima do foco. Nos espelhos convexos a imagem é virtual e menor do que o objeto, com a mesma orientação. Esses espelhos são usados em carros, cruzamentos de ruas e portas de garagem por terem um campo visual ampliado em relação a espelhos planos de mesmas dimensões.

Pense & Responda

Espelho convexo

Borges e Nicolau
1) Você observa a imagem de seu rosto num espelho esférico convexo. Afastando-se o espelho de seu rosto, a imagem que você vê:

• Aumenta ou diminui de tamanho?

• É sempre invertida ou sempre direita?

• Afasta-se ou aproxima-se do espelho?

2) Uma pequena lâmpada L é colocada em frente da superfície refletora de um espelho esférico convexo, de vértice V, foco principal F e centro de curvatura C. A imagem de L, formada pelo espelho, localiza-se em que ponto: A, B, D, E ou G?
x

Clique para ampliar

Dica do Blog

Crédito: R. Lucas ( STScI / AURA ), Hubble Heritage Team , NASA Lucas ( STScI / AURA ), da equipe do Hubble , da NASA. Clique para ampliar

Objeto de Hoag: Uma estranha galáxia em forma de anel

Para mais fotos de astronomia clique aqui

Arte do Blog

Obra de René François Ghislain Magritte (1898 - 1967)

Reflexos e reflexões
x
Borges e Nicolau
O quadro acima é de autoria do pintor belga René Magritte, um dos expoentes do surrealismo, corrente artística surgida em Paris nos anos da década de 1920 e que se caracteriza por buscar a representação do irracional e do subconsciente.
x
Magritte cuidava da forma com esmero, suas pinturas são de um realismo quase fotográfico, com um detalhe, tudo o que parece normal está repleto de anomalia.Os quadros do artista revelam empenho especial na criação de paradoxos visuais, a atração exercida pela obra fundamenta-se na tentativa de decifração das estranhezas que nos cercam. Com alguma dose daquele humor que produz sorrisos e inquietação ao mesmo tempo.
x
Dentre as inúmeras metáforas do artista destacamos o quadro do homem em frente ao espelho. Observe que há uma assimetria proposital na mensagem. O livro apoiado no anteparo sofre reflexão especular, com todos os detalhes que a caracterizam. O homem vê suas próprias costas através da reflexão no espelho. Seria essa uma superfície refletora capaz de revelar o oculto, o subjacente e, desmontando as leis da física, decifrar o grande mistério do Universo, sua própria existência?
x
Magritte, como todo grande artista nos induz à reflexão. E já que estamos falando de reflexão, vamos ver o que acontece na realidade, sem as sutilezas propostas pela magia do surrealismo.



Num espelho plano objeto e imagem têm as mesmas dimensões, equidistam do espelho, apresentam mesma orientação e naturezas opostas, isto é, se o objeto for real a imagem é virtual e vice-versa. Observe na foto a reflexão dos raios de luz que partem do rosto e incidem no espelho.

Leituras do Blog

Thomas Alva Edison (1847-1930)

Lâmpada elétrica por incandescência

xxxxxxxxxxxxxxxxxxxxx“Gênio é 1% inspiração e 99% transpiração”
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx(Thomas Alva Edison)

Quando você entra em seu quarto, um simples toque no interruptor faz com que a lâmpada acenda. Essa operação muito simples foi fruto de vários anos de pesquisa, que culminaram com a invenção da lâmpada elétrica por incandescência.

O funcionamento de uma lâmpada elétrica comum baseia-se no chamado efeito Joule ou efeito térmico da corrente elétrica: sempre que uma corrente elétrica atravessa um condutor, ocorrem colisões entre os elétrons que constituem a corrente e os átomos do condutor. Essas colisões fazem com que a energia elétrica se transforme em energia térmica, aquecendo o condutor, que pode tornar-se incandescente e emitir luz.

A lâmpada elétrica por incandescência é constituída por um bulbo de vidro, contendo um fio metálico, que se chama filamento, enrolado em forma de hélice com a finalidade de concentrar o calor produzido pela passagem da corrente elétrica. Dois fios metálicos ligam o filamento à rosca metálica e à base metálica.

O filamento é de tungstênio, cuja temperatura de fusão é elevada, cerca de 3.400ºC. Quando em funcionamento normal o filamento atinge temperaturas da ordem de 3.000ºC.

A lâmpada elétrica foi inventada em 1879 por Thomas Alva Edison (1847-1930). Ele utilizou, após inúmeras experiências, um filamento de carvão carbonizado, colocando-o numa ampola de vidro, da qual retirou o ar, fazendo vácuo, a fim de evitar que o filamento se queimasse. A lâmpada brilhou durante cerca de 40 horas.

A invenção de Thomas Edison sofreu inúmeros melhoramentos. Novos tipos de filamentos foram testados até se chegar ao de tungstênio. Quando se faz vácuo no interior das lâmpadas, evita-se que o filamento se queime, mas, por outro lado, facilita-se sua sublimação, isto é, a passagem direta do estado sólido para o estado gasoso. Para retardar a sublimação, introduz-se no bulbo uma pequena quantidade de gás nobre, o argônio.
(Do livro: “Eletricidade, História e Aplicações” de Nicolau Gilberto Ferraro)

Resolução do Desafio de Mestre de 18 / 08

Clique para ampliar

Condições de equilíbrio da barra:

x

1) A resultante das forças deve ser nula.

x

Em x:

x

Rx = 300 N (1)

x

Em y:

x

Ry = 50 + Q (2)

x

2) A somatória dos momentos das forças em relação ao ponto A deve ser nula:

x

-300.0,6l = 50.0,4l + Q.0,8l

180 = 20 + 0,8.Q

160 = 0,8.Q

x

Q = 200 N (3)

Resposta do ítem a.

x

Substituindo-se (3) em (2), vem:

x

Ry = 50 + 200

x

Ry = 250 N

x

A força que a articulação aplica na barra (R) pode ser calculada aplicando-se o teorema de Pitágoras:

R² = Rx² + Ry²

R² = 300² + 250²

R² = 90000 + 62500

R = √152500 N

A força que a articulação aplica na barra é aproximadamente

igual a 390 N.

Resposta do ítem b.

Resolução do Desafio de Mestre de 17 / 08

Clique para ampliar
Questão 1

Clique para ampliar
Questão 2

Clique para ampliar

Questão 3

Resolução do Desafio de Mestre de 16 / 08

Clique para ampliar

Questão 1

Clique para ampliar
Questão 2

Clique para ampliar
Questão 3

Eletrodinâmica

Como se calcula a energia elétrica consumida?

Borges e Nicolau
Conhecendo-se a potência P em quilowatt (kW) de um aparelho elétrico e o intervalo de tempo em horas (h) que ele fica ligado, podemos calcular a energia elétrica consumida E em quilowatt-hora (kWh), fazendo-se o produto:

E = P.Δt

Vamos supor que num dia frio você coloca a chave seletora do seu chuveiro elétrico na posição “inverno”. Considere que a potência elétrica do chuveiro seja de 5.600 W e que seu banho tenha a duração de 15 minutos. Vamos calcular a energia elétrica consumida:

P = 5600W = 5600/1000kW = 5,6kW e Δt = 15min = 1/4h, resulta:

Eel = P.Δt = 5,6kW.1/4h = 1,4kWh

Conhecendo-se o preço de 1kWh, pode-se calcular o custo da energia elétrica consumida durante o banho. Imagine que 1kWh custe R$0,40. A energia elétrica consumida durante o banho custa R$ 1,4.0,40, ou seja R$ 0,56.

Considerando uma casa com quatro pessoas, que tomam um banho por dia, temos o seguinte gasto mensal:

R$ 0,56.4.30 = > R$ 67,20

Passando a chave seletora para a posição “verão”, a potência do chuveiro diminui, por exemplo, para 3.200W:

P = 3200W = 3200/1000kW = 3,2kW. Durante um banho de 15min, ou seja, 1/4h , temos:

Eel = P.Δt = 3,2kW.1/4h = 0,8kWh.

Note, neste caso, que houve uma economia de energia por banho de 1,4kWh – 0,8kWh = 0,6kWh. Considerando a casa com 4 pessoas, teremos durante um mês a economia de energia igual a 0,6kWh.4.30 = 72kWh, correspondendo a R$ 28,80.

Pense e Responda

Quantas horas uma lâmpada de 60 W poderia ficar acessa se consumisse a mesma energia elétrica de um chuveiro elétrico de potência 4.500 W, durante um banho de 20 minutos?

Pesquise e Responda

No Sistema Internacional de Unidades (SI), a unidade de energia é o joule (J). Em Eletricidade é muito usada a unidade quilowatt-hora (kWh). Responda: 1 quilowatt-hora (kWh) corresponde a quantos joules (J)?

Óptica geométrica

De volta ao arco-íris

Borges e Nicolau
Ontem (dia 18/08/2010) apresentamos na Dica do Blog uma belíssima fotografia de um arco-íris. Como ele se forma?
x
Comecemos observando que o Sol deve estar próximo do horizonte, atrás da pessoa e devem existir gotas de água em suspensão na atmosfera. A luz solar incide nas gotas de água sofre refração com consequente dispersão, isto é, a luz solar ao se refratar sofre decomposição em suas cores componentes. A seguir, reflete nas paredes internas das gotas e novamente se refrata, voltando para o ar. A luz vermelha que emerge das gotas forma com a luz incidente um ângulo maior do que a luz violeta.
x

Clique para ampliar

Por isso, o observador recebe a luz vermelha do arco de gotas mais externo (maior ângulo) e luz violeta do arco mais interno (menor ângulo). Das gotas intermediárias recebe as demais cores.
x

Clique para ampliar

Desafio de Mestre

Clique para ampliar

x

Era uma vez uma placa

x

Borges e Nicolau
Uma placa de propaganda foi suspensa à extremidade B de uma barra homogênea, articulada na extremidade A. O peso da barra é de 50 N. O cabo horizontal é considerado ideal e suporta uma força de tração máxima de 300 N. O sistema está em equilíbrio na posição indicada na figura.
x

Sendo sen θ = 0,80 e cos θ = 0,60, determine:
x

a) O peso máximo da placa de propaganda.
b) A intensidade da força que a articulação exerce na barra, nas condições do item a.
x

(A resolução será publicada no próximo sábado, dia 21.)

Dica do Blog

Clique para ampliar

Arco-íris

A refração e a posterior reflexão da luz solar nas gotículas de chuva em suspensão no ar dão origem ao arco-íris. O arco mais externo é o vermelho e o mais interno é violeta. Na foto, nota-se um arco-íris secundário, mais externo que o arco-íris principal. O arco-íris secundário é formado devido a dupla reflexão da luz no interior das gotículas. Observe que no arco-íris secundário o arco mais externo é violeta e o mais interno é vermelho.

Para mais fotos de astronomia, clique aqui.

Momento, definição

Clique para ampliar

Como se calcula o momento de uma força em relação a um ponto?

Borges e Nicolau
Para o cálculo do momento MO de uma força F em relação a um ponto O devemos levar em conta a intensidade F da força e a distância d do ponto O à linha de ação da força. Por definição:

Mo = ± Fd

O momento pode ser positivo ou negativo. Adota-se, por convenção, o sinal (+) se a força F tende a girar o segmento OP em torno de O no sentido anti-horário e (-), no sentido horário.

O ponto O é denominado pólo, e a distância d, braço.

A unidade de momento no Sistema Internacional de Unidades (SI) é newton x metro (N . m).
Observação: No texto a notação em negrito, refere-se à grandeza vetorial.