Grandezas em Negrito, são Grandezas Vetoriais
1.
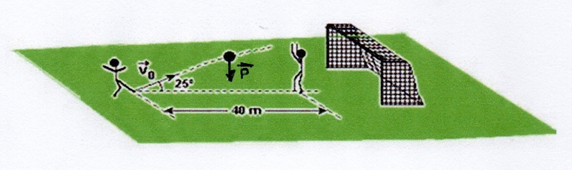
(UFJuiz de Fora) Durante uma partida de futebol, um jogador, percebendo que o goleiro do time adversário está longe do gol, resolve tentar um chute de longa distância (vide figura). O jogador se encontra a 40 m do goleiro. O vetor velocidade inicial da bola tem módulo Vo = 26 m/s e faz um ângulo de 25° com a horizontal, como mostra a figura a seguir.
Desprezando a resistência do ar, considerando a bola pontual e
usando cos 25° = 0,91, sen 25° = 0,42 e g=10m/s2:
a) Faça o diagrama de forças sobre a bola num ponto qualquer da
trajetória durante o seu voo, após ter sido chutada. Identifique a(s) força(s).
b) Saltando com os braços esticados, o goleiro pode atingir a
altura de 3,0 m. Ele consegue tocar a bola quando ela passa sobre ele?
Justifique.
c) Se a bola passar pelo goleiro, ela atravessará a linha de gol a
uma altura de 1,5 m do chão. A que distância o jogador se encontrava da linha
de gol, quando chutou a bola? (Nota: a linha de gol está atrás do goleiro.)
Resolução:
a)
Desprezada a resistência do ar, a única força
que age na bola é seu peso:
b) O movimento vertical é um MUV e o horizontal é um MU. Adotando
um sistema cartesiano de origem O no ponto de lançamento da bola, com eixo x
para a direita eixo y para cima, temos as equações:
x= v0x.t=>x=v0.cos25°.t = 26.0,91.t
=>x= 23,66.t (SI) (1)
y = v0y.t -5t2 =>y = v0.
sen25°.t -5t2=> y = 26.0,42.t-5t2 =>
y = 10,92.t -5t2(SI)(2)
De (1) para x = 40m, calculamos t; 40= 23,66.t=> t = 1,69s
Substituindo em (2), temos: y = 10,92.1,69 -5.(1,69)2=>
y = 18,45-14,28=> 4,17m :o goleiro não consegue agarrar a bola,
pois ela passa a 4,17 e o goleiro só consegue pular 3,0m.
c)De (2) para y=1,5m, temos: 1,5 = 10,92 t-5t2 =>
5t2 -10,92t + 1,5=0=> b2-4ac= (-10,92)2-4.5.1,5
=89,24 =>
(89,24)1/2 =
9,45
Raízes: t’= (10,92+9,45) /2.5 (s)=2,04s bola descendo, pois v<0
t” =
(10,92-9,45) /2.5 (s)= 0,15s bola subindo, pois v>0 substituindo-se t’ e t”
em (1), vem:
x’= 23,66.2,04 (m) = 48,27m quando a bola está descendo
x”=23,66.0,15 (m)= 3,55m bola subindo.
2.
Um goleiro lança a bola que atinge,
com velocidade de 10,0m/s, os pés do zagueiro de seu time, numa reta rente ao
gramado. O zagueiro devolve a bola ao goleiro com velocidade de 18km/h, na
mesma direção, mas em sentido contrário. A massa da bola é de 400g. Determine a
intensidade do impulso que o pé do zagueiro imprime à bola.
Resolução:
Pelo teorema do impulso temos;
I = Q2 -Q1
Em relação ao eixo adotado, vem:
I = mv2 –(-mv1) = m(v2 +v1)
Sendo: m= 0,40kg, v2=10,0m/s, v1=
18km/h = 5,0m/s, resulta:
I= 0,40kg. (10,0m/s +5,0m/s)=> I =2,0kg.m/s
3.
Resolução:
Vamos aplicar o teorema do Impulso:
IR= Q2 -Q1
Em módulo temos: Q1 =m. v1=0,40kg.15m/s=6,0
kg.m/s e Q2 =m. v2=0,40kg.20m/s=8,0 kg.m/s
De IR= Q2 -Q1 , vem : IR= Q2 + ( -Q1)
Em módulo: I2=(Q2)2+(Q1)2=36+64 => I = 10kg.m/s




Nenhum comentário:
Postar um comentário