Difração e Interferência
Fenômenos Ondulatórios
x
Borges e Nicolau
x
Já estudamos os fenômenos da reflexão e refração. Vamos analisar mais alguns fenômenos ondulatórios.
x
1. Superposição de pulsos
xxxxxxxxx
Considere dois pulsos que se propagam em sentidos opostos em uma corda tensa. Ocorre interferência ou superposição quando os dois pulsos atingem simultaneamente o mesmo ponto P da corda. Admita que os pulsos tenham mesma largura e amplitudes a1 e a2 e vamos analisar dois tipos particulares de interferência:
x
1°) Interferência construtiva: A amplitude do pulso resultante é a soma das amplitudes dos pulsos que se superpõem: a = a1 + a2
x
2º) Interferência destrutiva: A amplitude do pulso resultante é a diferença entre as amplitudes dos pulsos que se superpõem: a = a1 - a2
x
Após a superposição cada pulso continua sua propagação como se nada tivesse ocorrido. Observação: No caso em que a1 = a2, resulta a = 0 e a interferência destrutiva é total.
x
x
2. Ondas estacionárias
x
A superposição de ondas periódicas obedece os mesmos princípios da superposição de pulsos. As ondas estacionárias resultam da superposição de ondas periódicas iguais e que se propagam em sentidos opostos. Obtém-se ondas estacionárias em uma corda tensa pela superposição da onda periódica produzida numa extremidade com a onda refletida na extremidade fixa.
1º) Pontos que não vibram (amplitude Amínimo = 0). Nestes pontos, denominados nós, ocorrem interferências destrutivas.
2º) Pontos que vibram com máxima amplitude (Amáximo = 2a). Nestes pontos, denominados ventres, ocorrem interferências construtivas.
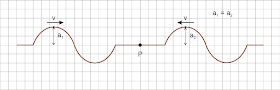
3º) Pontos que vibram entre os nós e os ventres com amplitudes entre 0 e 2a. Sendo λ o comprimento de onda das ondas que interferem, podemos concluir que a distância entre dois nós consecutivos é igual a λ/2; entre dois ventres consecutivos é também λ/2; já entre um nó e um ventre consecutivo é λ/4. A figura em linha contínua representada acima é a envoltória das posições da corda em vibração (linhas tracejadas). Quando a corda vibra muito rapidamente, percebemos apenas a envoltória. A formação ondas estacionárias não ocorrem somente com ondas propagando-se em cordas, mas também com ondas sonoras, luminosas, ondas que se propagam na superfície de um líquido etc.
3. Difração
É o fenômeno que consiste em uma onda contornar um obstáculo. Vamos, por exemplo, produzir uma perturbação batendo com uma régua na superfície da água tranquila de um tanque. Forma-se uma onda reta que ao atingir uma barreira dotada de uma fenda, espalha-se em todas as direções a partir da fenda. A explicação da difração é dada pelo Princípio de Huygens: cada ponto da frente de onda que atravessa a fenda comporta-se como uma fonte de ondas secundárias.
Recorde pela animação a superposição de pulsos.
Clique aqui
Exercícios básicos:
Exercício 1:
Dois pulsos são produzidos em uma corda tensa conforme indica a figura. Faça um esquema mostrando o pulso resultante quando os pulsos parciais estiverem exatamente superpostos (crista com crista, vale com vale).
x
Resolução: clique aqui
x
Exercício 2:
A figura representa dois pulsos propagando-se num mesmo meio e em sentidos opostos. Eles superpõem-se no ponto P desse meio. Qual é o deslocamento do ponto P no instante da superposição? Analise os casos a), b) e c).
x
Resolução: clique aqui
xxxxxxx
Exercício 3:
Uma corda tensa de 1,0 m de comprimento vibra com frequência de 10 Hz. A onda estacionária que se estabelece na corda tem o aspecto indicado na figura. Determine o comprimento de onda e a velocidade de propagação das ondas que se superpõem.
x
x
Resolução: clique aqui
xxxxxxx
Exercício 4:
Ondas estacionárias são produzidas numa corda tensa de comprimento 1,2 m e fixa em suas extremidades. Observa-se a formação de 7 nós no total. Qual é o comprimento de onda das ondas que se superpõem?
xxxxxxx
Resolução: clique aqui
xxxxxxx
Exercício 5:
Você conversa com seu vizinho embora um muro de 2,5 m de altura os separe. Isto é possível devido o fenômeno da:
a) reflexão;
b) refração;
c) difração;
d) superposição de ondas;
e) absorção das ondas pelo ar atmosférico.
xxxxx
Resolução: clique aqui
Exercícios de Revisão
Revisão/Ex 1:
(UFC-CE)
A figura I mostra, no instante t = 0, dois pulsos retangulares que se propagam em sentidos contrários, ao longo de uma corda horizontal esticada. A velocidade de cada pulso tem módulo igual a 2,0 cm/s. O pulso da esquerda tem 3,0 cm de largura e o da direita, 1,0 cm. Dentre as opções seguintes indique aquela que mostra o perfil da corda no instante t = 2,0 s.
Resolução: clique aqui
Revisão/Ex 2:
(UFRJ)
Uma onda na forma de um pulso senoidal tem altura máxima de 2,0 cm e se propaga para a direita com velocidade de 1,0.104 cm/s, num fio esticado e preso a uma parede fixa (figura 1). No instante considerado inicial, a frente de onda está a 50 cm da parede.
Determine o instante em que a superposição da onda incidente com a refletida tem a forma mostrada na figura 2, com altura máxima de 4,0 cm.
Resolução: clique aqui
Revisão/Ex 3:
(UFPB)
A superposição de ondas incidentes e refletidas com mesmas amplitudes, dá origem a uma figura de interferência denominada onda estacionária. Nesse sentido, considere uma situação em que uma corda tem uma das suas extremidades fixa a uma parede e a outra extremidade, conectada a um oscilador (fonte de vibração) que vibra com uma frequência de 80 Hz. A distância entre o vibrador e a parede é de 8,0 m.
Sabendo que as velocidades de propagação das ondas na corda são de 320 m/s, a onda estacionária na corda está melhor representada na figura:
Revisão/Ex 4:
(UFTM)
Sílvia e Patrícia brincavam com uma corda quando perceberam que, prendendo uma das pontas num pequeno poste e agitando a outra ponta em um mesmo plano, faziam com que a corda oscilasse de forma que alguns de seus pontos permaneciam parados, ou seja, se estabelecia na corda uma onda estacionária.
A figura 1 mostra a configuração da corda quando Sílvia está brincando e a figura 2 mostra a configuração da mesma corda quando Patrícia está brincando.
Considerando-se iguais, nas duas situações, as velocidades de propagação das ondas na corda, e chamando de fS e fP as frequências com que Sílvia e Patrícia, respectivamente, estão fazendo a corda oscilar, pode-se afirmar corretamente que a relação fS / fP é igual a
a) 1,6.
b) 1,2.
c) 0,8.
d) 0,6.
e) 0,4.
Resolução: clique aqui
Revisão/Ex 5:
(Vunesp-SP)
A figura a seguir representa esquematicamente as frentes de onda de uma onda reta na superfície da água, propagando-se da região 1 para a região 2. Essas regiões são idênticas e separadas por uma barreira com abertura.
A configuração das frentes de onda observada na região 2, que mostra o que aconteceu com a onda incidente ao passar pela abertura, caracteriza o fenômeno da:
a) absorção.
b) difração.
c) dispersão.
d) polarização.
e) refração.
Resolução: clique aqui
b
Desafio:
Dois pulsos, A e B, são produzidos em uma corda esticada, que tem uma extremidade fixada numa parede, conforme mostra a figura. Os pulsos se propagam com velocidade de 20 m/s.
Responda:
a) que tipo de superposição ocorre, após o pulso A ter sofrido reflexão na parede: construtiva ou destrutiva?
b) qual é a velocidade do pulso A no instante da superposição?
A resolução será publicada na próxima terça-feira
Resolução do desafio anterior:
Uma corda é feita de um material de densidade d = 5,0 kg/m3 e tem seção transversal de área A = 1,0.102 cm2. A corda está sendo tracionada, numa extremidade, por uma força de intensidade F = 2,0.10-3 N. A outra extremidade da corda efetua um MHS de frequência f = 4,0 Hz. Determine:
a) a densidade linear μ da corda;
b) a velocidade v de propagação das ondas na corda;
c) o comprimento de onda λ.
Resolução:
Seja L o comprimento da corda e m sua massa. Seu volume é dado por: V = A.L, onde A é a área da seção transversal da corda. Podemos escrever:
d = m/V => d = m/A.L => d = μ/A => μ = d.A =>
μ = (5,0kg/m3).(1,0.102.10-4 m2) => μ = 5,0.10-2 kg/m
b)
v = √(F/μ) => v = √(2,0.10-3N)/(5,0.10-2kg/m) =>
v = 2,0.10-1 m/s = 20 cm/s
c)
v = λ.f => 2,0.10-1m/s = λ.4,0Hz => λ = 5,0.10-2 m = 5,0 cm
Respostas:
a) 5,0.10-2 kg/m; b) 20 cm/s; c) 5,0 cm














Nenhum comentário:
Postar um comentário