A necessidade do ser humano de compreender o ambiente que o cerca e explicar os fenômenos naturais é a gênese da Física.
sexta-feira, 30 de novembro de 2018
quinta-feira, 29 de novembro de 2018
Caiu no vestibular
Na gravidade da Lua
(AFA-SP)
Em uma experiência realizada na Lua uma pedra é lançada verticalmente para cima e, no mesmo instante, outra pedra é abandonada de uma altura de 40 m. Sabendo-se que as pedras colidem a 20 m de altura e que a aceleração da gravidade na Lua é de 1,6 m/s2, a velocidade com que foi lançada a primeira pedra tem módulo, em m/s, igual a:
a) 2,0 b) 4,0 c) 6,0 d) 8,0
Resolução:
Orientando-se a trajetória para cima e adotando-se a origem dos espaços no solo, temos:
Pedra P1: s1 = v0.t-g.t2/2
Pedra P2: s2 = 40-g.t2/2
Encontro: 40-g.t2/2 = v0.t-g.t2/2 => 40 = v0.t (1)
Mas no encontro s2 = 20 m => 40-g.t2/2 = 20 => g.t2/2 = 20 =>
t = √(40/1,6) => t = 5,0 s (2)
(2) em (1): 40 = v0.5,0 => v0 = 8,0 m/s
Resposta: b
quarta-feira, 28 de novembro de 2018
Cursos do Blog - Eletricidade
Em determinados fenômenos, a luz apresenta natureza corpuscular
e em outros, natureza ondulatória. É o caráter dual da luz.
37ª aula
O caráter dual da luz
Borges e Nicolau
O cientista holandês Christian Huygens (1629-1695) apresentou a teoria ondulatória da luz, segundo a qual a luz se propaga através do espaço por meio de ondas.
O caráter ondulatório da luz ficou plenamente estabelecido quando o físico escocês John Clerk Maxwell (1831-1879) formulou a teoria ondulatória eletromagnética, considerando a luz uma onda eletromagnética.
A teoria ondulatória justifica muitos fenômenos que ocorrem com a luz, como é o caso da interferência e da difração.
No entanto, o efeito fotoelétrico explicado por Einstein considera a luz como um fluxo de “partículas” ou “corpúsculos”, denominados fótons.
Ao colidir com a superfície de um metal as "partículas de luz" (fótons)podem "arrancar" elétrons desta superfície. Esse fenômeno é chamado de efeito fotoelétrico, resultando da colisão entre duas “partículas”, o fóton e o elétron.
A luz apresenta, portanto, dupla natureza: ondulatória e corpuscular, comportando-se como onda eletromagnética ou como fluxo de partículas, conforme o fenômeno estudado.
É esse o caráter dual de luz.
Como a luz pode se comportar como onda ou como “partícula”, o físico francês Louis De Broglie (1892–1987) apresentou, em 1924, a seguinte hipótese: partículas também possuem propriedades ondulatórias.
O comprimento de onda associado à partícula, denominado comprimento de onda de De Broglie, é dado por:
A quantidade de movimento m.v evidencia o caráter corpuscular, enquanto o comprimento de onda λ evidencia o caráter ondulatório.
Em 1927 cientistas dos laboratórios Bell, nos Estados Unidos, constataram um fenômeno até então considerado exclusivamente ondulatório: a difração de elétrons. Conclui-se, então, que partículas também apresentam propriedades ondulatórias, o que confirma hipótese formulada por Louis De Broglie.
Exercícios básicos
Exercício 1:
Analise as proposições:
I) Em determinados fenômenos a luz apresenta natureza ondulatória e, em outros, corpuscular. É o caráter dual da luz.
II) Os fenômenos da interferência da luz, da difração e o efeito fotoelétrico são explicados pela natureza ondulatória da luz.
III) Partículas, como os elétrons, também possuem propriedades ondulatórias.
Tem-se:
a) só I) é correta;
b) só II) é correta;
c) só III) é correta;
d) só I) e III) são corretas;
e) I), II) e III) são corretas.
Resolução: clique aqui
Exercício 2:
Um elétron se desloca com velocidade 3,0.106 m/s. Determine o comprimento de onda de De Broglie associado ao elétron.Dados: massa do elétron m = 9,11.10-31 kg
constante de Planck h = 6,63.10-34 J.s.
Resolução: clique aqui
Exercício 3:
Uma bola de futebol se desloca com velocidade 10 m/s. Calcule o comprimento de onda de De Broglie associado à bola.
Dados: massa da bola de futebol m = 400 g
constante de Planck h = 6,63.10-34 J.s.
Resolução: clique aqui
Exercício 4:
Retome os dois últimos exercícios anteriores. Por meio dos valores dos comprimentos de onda associados ao elétron e à bola de futebol, explique por que não se pode observar efeitos ondulatórios, como a difração, para objetos em escala macroscópica.
Resolução: clique aqui
Exercícios de Revisão
Revisão/Ex 1:
(UFRN)
Bárbara ficou encantada com a maneira de Natasha explicar a dualidade onda-partícula, apresentada nos textos de Física Moderna. Natasha fez uma analogia com o processo de percepção de imagens, apresentando uma explicação baseada numa figura muito utilizada pelos psicólogos da Gestalt. Seus esclarecimentos e a figura ilustrativa são reproduzidos a seguir:
Figura citada por Natasha, na qual dois perfis formam um cálice e vice-versa.
A minha imagem preferida sobre o comportamento dual da luz é o desenho de um cálice feito por dois perfis. Qual a realidade que percebemos na figura? Podemos ver um cálice ou dois perfis, dependendo de quem consideramos como figura e qual consideraremos como fundo, mas não podemos ver ambos simultaneamente. É um exemplo perfeito de realidade criada pelo observador, em que nós decidimos o que vamos observar. A luz se comporta de forma análoga, pois, dependendo do tipo de experiência ("fundo"), revela sua natureza de onda ou sua natureza de partícula, sempre escondendo uma quando a outra é mostrada.
Diante das explicações acima, é correto afirmar que Natasha estava ilustrando, com o comportamento da luz, o que os físicos chamam de princípio da:
a) incerteza de Heisenberg.
b) complementaridade de Bohr.
c) superposição.
d) relatividade.
Resolução: clique aqui
Revisão/Ex 2:
(URGS-RS)
O dualismo onda-partícula refere-se a características corpusculares presentes nas ondas luminosas e a características ondulatórias presentes no comportamento de partículas, tais como elétrons. A natureza nos mostra que características corpusculares e ondulatórias não são antagônicas mas, sim, complementares. Dentre os fenômenos listados, o único que não está relacionado com o dualismo onda-partícula é:
a) o efeito fotoelétrico.
b) a ionização de átomos pela incidência de luz.
c) a difração de elétrons.
d) o rompimento de ligações entre átomos pela incidência de luz.
e) propagação, no vácuo, de ondas de rádio de frequência média.
Resolução: clique aqui
Revisão/Ex 3:
(UFC-CE)
Associamos a uma partícula material o que chamamos de comprimento de onda de De Broglie.
A) Dê a expressão que relaciona o comprimento de onda de De Broglie com o momentum da partícula.
B) Considere duas partículas com massas diferentes e mesma velocidade. Podemos associar a cada uma o mesmo comprimento de onda de De Broglie? Justifique.
Revisão/Ex 4:
(Olimpíada Paulista de Física)
Cálcule o momento linear de um fóton de comprimento de onda 780 nm, típico de diodos laser empregados na leitura de CDs.
Dado: h = constante de Planck = 6,63.10-34 J.s
a) 2,5.10-27 J.s/m
b) 3,5.10-28 J.s/m
c) 4,5.10-26 J.s/m
d) 8,5.10-28 J.s/m
e) 9,5.10-29 J.s/m
Resolução: clique aqui
b
Louis-Victor de Broglie
Louis-Victor de Broglie, físico francês, nasceu em 1892. Em 1909 completou o ensino secundário. Fez o curso de História na Sorbonne, pretendendo dedicar-se à carreira diplomática. Durante a I Guerra Mundial, de Broglie serviu ao exército. Após a guerra interessou-se pelo estudo de Matemática e Física, por influência de seu irmão, Maurice de Broglie. Estudou Mecânica Quântica e realizou pesquisas sobre os Raios-X. Em 1924, na Faculdade de Ciências da Universidade de Paris, defendeu sua tese de doutoramento desenvolvendo o tema “Pesquisas sobre a teoria quântica”. Neste trabalho apresenta a seguinte hipótese: partículas também possuem propriedades ondulatórias e consequentemente, apresentam um comprimento de onda característico, denominado comprimento de onda de de Broglie, dado por:xλx=xh/(m.v).
Louis-Victor de Broglie recebeu o Prêmio Nobel de Física de 1929 pelo trabalho sobre a dualidade onda-partícula.
Questão:
Calcule o comprimento de onda de de Broglie nas duas situações descritas abaixo:
a) para um elétron, deslocando-se com velocidade 40 m/s.
b) para uma pessoa de massa 60 kg, deslocando-se com velocidade 40 m/s.
c) em vista dos resultados obtidos, explique por que não podemos observar efeitos ondulatórios para objetos em escala macroscópica.
Dados:
constante de Planck: h = 6,63.10-34 J.s;
massa do elétron: me = 9,1.10-31 kg.
A resolução será publicada na próxima quarta-feira.
Uma superfície de potássio é iluminada com luz de comprimento de onda 300 nm. A função trabalho do potássio é igual a 2,24 eV. Determine:
a) a energia cinética máxima para os fotoelétrons emitidos;
b) o comprimento de onda de corte.
Dados:
constante de Planck:
h = 4,14.10-15 eV.s.
velocidade de propagação da radiação eletromagnética no vácuo:
c = 3,0.108 m/s
a)
Equação fotoelétrica de Einstein:
EC = hf - Φ => Ec = h.(c/λ) - Φ =>
EC = 4,14.10-15.(3,0.108/300.10-9) - 2,24 => EC = 1,90 eV
EC = hf - Φ => Ec = h.(c/λ) - Φ =>
EC = 4,14.10-15.(3,0.108/300.10-9) - 2,24 => EC = 1,90 eV
b)
c = λ0.f0 => c = λ0.Φ/h => λ0 = c.h/Φ =>
λ0 = (3,0.108m/s).(4,14.10-15eV)/2,24eV => λ0 ≅ 554 nm
Respostas: a) 1,90 eV; b) 554 nm
Respostas: a) 1,90 eV; b) 554 nm
terça-feira, 27 de novembro de 2018
Cursos do Blog - Termologia, Óptica e Ondas
Difração e Interferência
Fenômenos Ondulatórios
x
Borges e Nicolau
x
Já estudamos os fenômenos da reflexão e refração. Vamos analisar mais alguns fenômenos ondulatórios.
x
1. Superposição de pulsos
xxxxxxxxx
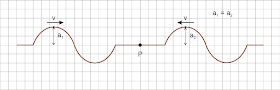
Considere dois pulsos que se propagam em sentidos opostos em uma corda tensa. Ocorre interferência ou superposição quando os dois pulsos atingem simultaneamente o mesmo ponto P da corda. Admita que os pulsos tenham mesma largura e amplitudes a1 e a2 e vamos analisar dois tipos particulares de interferência:
x
1°) Interferência construtiva: A amplitude do pulso resultante é a soma das amplitudes dos pulsos que se superpõem: a = a1 + a2
x
2º) Interferência destrutiva: A amplitude do pulso resultante é a diferença entre as amplitudes dos pulsos que se superpõem: a = a1 - a2
x
Após a superposição cada pulso continua sua propagação como se nada tivesse ocorrido. Observação: No caso em que a1 = a2, resulta a = 0 e a interferência destrutiva é total.
x
x
2. Ondas estacionárias
x
A superposição de ondas periódicas obedece os mesmos princípios da superposição de pulsos. As ondas estacionárias resultam da superposição de ondas periódicas iguais e que se propagam em sentidos opostos. Obtém-se ondas estacionárias em uma corda tensa pela superposição da onda periódica produzida numa extremidade com a onda refletida na extremidade fixa.
1º) Pontos que não vibram (amplitude Amínimo = 0). Nestes pontos, denominados nós, ocorrem interferências destrutivas.
2º) Pontos que vibram com máxima amplitude (Amáximo = 2a). Nestes pontos, denominados ventres, ocorrem interferências construtivas.
3º) Pontos que vibram entre os nós e os ventres com amplitudes entre 0 e 2a. Sendo λ o comprimento de onda das ondas que interferem, podemos concluir que a distância entre dois nós consecutivos é igual a λ/2; entre dois ventres consecutivos é também λ/2; já entre um nó e um ventre consecutivo é λ/4. A figura em linha contínua representada acima é a envoltória das posições da corda em vibração (linhas tracejadas). Quando a corda vibra muito rapidamente, percebemos apenas a envoltória. A formação ondas estacionárias não ocorrem somente com ondas propagando-se em cordas, mas também com ondas sonoras, luminosas, ondas que se propagam na superfície de um líquido etc.
3. Difração
É o fenômeno que consiste em uma onda contornar um obstáculo. Vamos, por exemplo, produzir uma perturbação batendo com uma régua na superfície da água tranquila de um tanque. Forma-se uma onda reta que ao atingir uma barreira dotada de uma fenda, espalha-se em todas as direções a partir da fenda. A explicação da difração é dada pelo Princípio de Huygens: cada ponto da frente de onda que atravessa a fenda comporta-se como uma fonte de ondas secundárias.
Recorde pela animação a superposição de pulsos.
Clique aqui
Exercícios básicos:
Exercício 1:
Dois pulsos são produzidos em uma corda tensa conforme indica a figura. Faça um esquema mostrando o pulso resultante quando os pulsos parciais estiverem exatamente superpostos (crista com crista, vale com vale).
x
Resolução: clique aqui
x
Exercício 2:
A figura representa dois pulsos propagando-se num mesmo meio e em sentidos opostos. Eles superpõem-se no ponto P desse meio. Qual é o deslocamento do ponto P no instante da superposição? Analise os casos a), b) e c).
x
Resolução: clique aqui
xxxxxxx
Exercício 3:
Uma corda tensa de 1,0 m de comprimento vibra com frequência de 10 Hz. A onda estacionária que se estabelece na corda tem o aspecto indicado na figura. Determine o comprimento de onda e a velocidade de propagação das ondas que se superpõem.
x
x
Resolução: clique aqui
xxxxxxx
Exercício 4:
Ondas estacionárias são produzidas numa corda tensa de comprimento 1,2 m e fixa em suas extremidades. Observa-se a formação de 7 nós no total. Qual é o comprimento de onda das ondas que se superpõem?
xxxxxxx
Resolução: clique aqui
xxxxxxx
Exercício 5:
Você conversa com seu vizinho embora um muro de 2,5 m de altura os separe. Isto é possível devido o fenômeno da:
a) reflexão;
b) refração;
c) difração;
d) superposição de ondas;
e) absorção das ondas pelo ar atmosférico.
xxxxx
Resolução: clique aqui
Exercícios de Revisão
Revisão/Ex 1:
(UFC-CE)
A figura I mostra, no instante t = 0, dois pulsos retangulares que se propagam em sentidos contrários, ao longo de uma corda horizontal esticada. A velocidade de cada pulso tem módulo igual a 2,0 cm/s. O pulso da esquerda tem 3,0 cm de largura e o da direita, 1,0 cm. Dentre as opções seguintes indique aquela que mostra o perfil da corda no instante t = 2,0 s.
Resolução: clique aqui
Revisão/Ex 2:
(UFRJ)
Uma onda na forma de um pulso senoidal tem altura máxima de 2,0 cm e se propaga para a direita com velocidade de 1,0.104 cm/s, num fio esticado e preso a uma parede fixa (figura 1). No instante considerado inicial, a frente de onda está a 50 cm da parede.
Determine o instante em que a superposição da onda incidente com a refletida tem a forma mostrada na figura 2, com altura máxima de 4,0 cm.
Resolução: clique aqui
Revisão/Ex 3:
(UFPB)
A superposição de ondas incidentes e refletidas com mesmas amplitudes, dá origem a uma figura de interferência denominada onda estacionária. Nesse sentido, considere uma situação em que uma corda tem uma das suas extremidades fixa a uma parede e a outra extremidade, conectada a um oscilador (fonte de vibração) que vibra com uma frequência de 80 Hz. A distância entre o vibrador e a parede é de 8,0 m.
Sabendo que as velocidades de propagação das ondas na corda são de 320 m/s, a onda estacionária na corda está melhor representada na figura:
Revisão/Ex 4:
(UFTM)
Sílvia e Patrícia brincavam com uma corda quando perceberam que, prendendo uma das pontas num pequeno poste e agitando a outra ponta em um mesmo plano, faziam com que a corda oscilasse de forma que alguns de seus pontos permaneciam parados, ou seja, se estabelecia na corda uma onda estacionária.
A figura 1 mostra a configuração da corda quando Sílvia está brincando e a figura 2 mostra a configuração da mesma corda quando Patrícia está brincando.
Considerando-se iguais, nas duas situações, as velocidades de propagação das ondas na corda, e chamando de fS e fP as frequências com que Sílvia e Patrícia, respectivamente, estão fazendo a corda oscilar, pode-se afirmar corretamente que a relação fS / fP é igual a
a) 1,6.
b) 1,2.
c) 0,8.
d) 0,6.
e) 0,4.
Resolução: clique aqui
Revisão/Ex 5:
(Vunesp-SP)
A figura a seguir representa esquematicamente as frentes de onda de uma onda reta na superfície da água, propagando-se da região 1 para a região 2. Essas regiões são idênticas e separadas por uma barreira com abertura.
A configuração das frentes de onda observada na região 2, que mostra o que aconteceu com a onda incidente ao passar pela abertura, caracteriza o fenômeno da:
a) absorção.
b) difração.
c) dispersão.
d) polarização.
e) refração.
Resolução: clique aqui
b
Desafio:
Dois pulsos, A e B, são produzidos em uma corda esticada, que tem uma extremidade fixada numa parede, conforme mostra a figura. Os pulsos se propagam com velocidade de 20 m/s.
Responda:
a) que tipo de superposição ocorre, após o pulso A ter sofrido reflexão na parede: construtiva ou destrutiva?
b) qual é a velocidade do pulso A no instante da superposição?
A resolução será publicada na próxima terça-feira
Resolução do desafio anterior:
Uma corda é feita de um material de densidade d = 5,0 kg/m3 e tem seção transversal de área A = 1,0.102 cm2. A corda está sendo tracionada, numa extremidade, por uma força de intensidade F = 2,0.10-3 N. A outra extremidade da corda efetua um MHS de frequência f = 4,0 Hz. Determine:
a) a densidade linear μ da corda;
b) a velocidade v de propagação das ondas na corda;
c) o comprimento de onda λ.
Resolução:
Seja L o comprimento da corda e m sua massa. Seu volume é dado por: V = A.L, onde A é a área da seção transversal da corda. Podemos escrever:
d = m/V => d = m/A.L => d = μ/A => μ = d.A =>
μ = (5,0kg/m3).(1,0.102.10-4 m2) => μ = 5,0.10-2 kg/m
b)
v = √(F/μ) => v = √(2,0.10-3N)/(5,0.10-2kg/m) =>
v = 2,0.10-1 m/s = 20 cm/s
c)
v = λ.f => 2,0.10-1m/s = λ.4,0Hz => λ = 5,0.10-2 m = 5,0 cm
Respostas:
a) 5,0.10-2 kg/m; b) 20 cm/s; c) 5,0 cm