Exercício 1:
(UNICAMP)
Recentemente, a sonda New Horizons tornou-se a primeira espaçonave a sobrevoar Plutão, proporcionando imagens espetaculares desse astro distante.
a) A sonda saiu da Terra em janeiro de 2006 e chegou a Plutão em julho de 2015. Considere que a sonda percorreu uma distância de 4,5 bilhões de quilômetros nesse percurso e que 1 ano é aproximadamente 3x107 s. Calcule a velocidade escalar média da sonda nesse percurso.
b) A sonda New Horizons foi lançada da Terra pelo veículo espacial Atlas V 511, a partir do Cabo Canaveral. O veículo, com massa total m = 6.105 kg, foi o
objeto mais rápido a ser lançado da Terra para o espaço até o momento. O trabalho realizado pela força resultante para levá-lo do repouso à sua velocidade
máxima foi de τ = 768.1011 J. Considerando que a massa total do veículo não variou durante o lançamento, calcule sua velocidade máxima.
Resolução:
a)
Δt = 9,5 anos = 9,5.3.107s = 2,85.108 s
Δs = 4,5.109 km
vm = Δs/Δt = 4,5.109km/2,85.108s => vm ≅ 15,8 km/s
b)
Teorema da energia cinética
τres = m.V2/2 - mV02/2
768.1011 = (6.1015/2).V2máx
Vmáx = 16.103 m/s = 16 km/s
Respostas: a) 15,8 km/s; b) 16 km/s
Exercício 2:
FMJ (Faculdade de Medicina de Jundiaí)
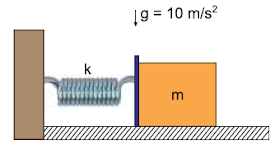
A figura mostra uma mola ideal, de constante elástica k = 100 N/m, com uma extremidade fixa numa parede e a outra encostada a um bloco de massa m = 5 kg, apoiado sobre uma superfície plana e horizontal.
O coeficiente de atrito estático e o coeficiente de atrito cinético entre o bloco e a superfície de apoio são iguais a 0,5 e 0,4, respectivamente.
a) Determine a compressão máxima da mola, em metros, que mantém o bloco em equilíbrio estático.
b) Considerando a resistência do ar desprezível e que o bloco tenha partido do repouso quando a mola estava comprimida de 0,50 m, calcule a velocidade do bloco, em m/s, no instante em que ele perde contato com a mola.
Resolução:
a)
F = Fat => F = μ.FN = μ.P = 0,5.50 ∴ F = 25 N
F = kx => 25 = 100.x ∴ x = 0,25 m = 25 cm
b)
Teorema da energia cinética
τres = m.v2/2 - mv02/2
τF + τFat = m.v2/(2-0)
kd2/2 - μP.d = m.v2/2
100.(0,50)2/2 - 0,40.50.0,50 = 5.v2/2
v = 1,0 m/s
Respostas: a) 25 cm; b) 1,0 m/s
Exercício 3:
(Escola Naval)
Observe a figura a seguir.
Um caixote pesando 50 N, no instante t = 0, se encontra em repouso sobre um plano muito longo e inclinado de 30° em relação à horizontal. Entre o caixote e o plano inclinado, o coeficiente de atrito estático é 0,20 e o cinético é 0,10. Sabe-se que a força F, paralela ao plano inclinado, conforme indica a figura acima, tem intensidade igual a 36 N. No instante t = 9 s, qual o módulo, em newtons, da força de atrito entre o caixote e o plano? Nesse mesmo instante, o bloco estará subindo, descendo ou permanece em repouso sobre o plano inclinado?
(A) 14 e descendo.
(B) 11 e permanece em repouso.
(C) 9,0 e subindo.
(D) 8,5 e permanece em repouso.
(E) 4,5 e subindo.
Dados:
sen 30° = 0,5
cos 30° = 0,9
Resolução:
Cálculo da força de atrito estática máxima
Fatmáx = μe.P.cos30° = 0,20.50.0,9 ∴ Fatmáx = 9,0 N
Pt = P.sen30° = 50.0,5 ∴ Pt = 25 N
Sendo F = 36 N > Fatmáx + P = 34 N, concluímos que o caixote está subindo.
Durante o movimento a força de atrito é a dinâmica:
FatD = μD.P.cos30° = 0,10.50.0,9 portanto FatD = 4,5 N
Resposta: (E)
Exercício 4:
(Unesp)
O gol da conquista do tetracampeonato pela Alemanha na Copa do Mundo de 2014 foi feito pelo jogador Götze. Nessa jogada, ele recebeu um cruzamento, matou a bola no peito, amortecendo-a, e chutou de esquerda para fazer o gol. Considere que, imediatamente antes de tocar o jogador, a bola tinha velocidade de módulo V1 = 8 m/s em uma direção perpendicular ao seu peito e que, imediatamente depois de tocar o jogador, sua velocidade manteve-se perpendicular ao peito do jogador, porém com módulo V = 0,6 m/s e em sentido contrário.
Admita que, nessa jogada, a bola ficou em contato com o peito do jogador por 0,2 s e que, nesse intervalo de tempo a intensidade da força resultante (FR), que atuou sobre ela, variou em função do tempo, conforme o gráfico
Considerando a massa da bola igual a 0,4 kg, é correto afirmar que, nessa jogada, o módulo da força resultante máxima que atuou sobre a bola, indicada no gráfico por Fmáx, é igual, em newtons, a
a) 68,8
b) 34,4
c) 59,2
d) 26,4
e) 88,8
Teorema do Impulso:
Ires = mv2 - m(-v1)
Sendo Ires numericamente igual à área do triângulo, temos:
0,2.Fmáx/2 = 0,4.(0,6+8)
Fmáx = 34,4 N
Resposta: b
Na próxima semana apresentaremos novas questões.




Nenhum comentário:
Postar um comentário