39° aula - (última aula do 2º semestre)
Cordas vibrantes / Tubos sonoros
As cordas vibrantes
Ao percutirmos a corda tensa de um violão as ondas transversais produzidas refletem-se nas extremidades e superpõem-se ao longo da corda, formando ondas estacionárias. Com a vibração da corda, o ar em suas vizinhanças também vibra originando ondas sonoras. A frequência do som emitido é igual à frequência de vibração da corda.
O modo mais simples de a corda vibrar corresponde a um nó em cada extremidade e entre eles um único ventre. É o chamado modo fundamental ou primeiro harmônico. Nesta situação a frequência de vibração é denominada frequência fundamental ou frequência do primeiro harmônico. Indicando por n o número de ventres, temos neste caso n = 1.
Sendo L ao comprimento da corda, obtemos:
Seja v a velocidade das ondas que se propagam na corda e que originam as ondas estacionárias. A frequência fundamental será:
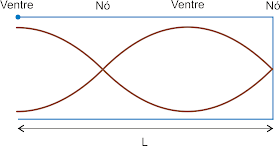
Obtemos o segundo modo de vibração acrescentando mais um nó e mais um ventre (total, dois ventres: n = 2). Temos assim o segundo harmônico.
Neste caso, temos:
Para o harmônico de ordem n, isto é para n ventres, teremos:
(n = 1, 2, 3, 4, 5...)
Recordando: Velocidade de propagação de uma onda transversal numa corda tensa
Considere uma corda de massa m e comprimento L e sob ação de uma força de tração de intensidade F.
Densidade linear da corda é a grandeza μ definida pela relação entre a massa m da corda e o seu comprimento L:
A velocidade de propagação da onda na corda é dada por:
Os tubos sonoros
Os tubos sonoros podem ser abertos ou fechados
Pela embocadura o ar soprado adequadamente produz vibração no interior do tubo, a qual se propaga e se reflete nas extremidades originando a formação de ondas estacionárias.
A embocadura de um tubo sonoro é sempre um ventre. A outra extremidade é um ventre de vibração se o tubo for aberto e um nó se o tubo for fechado. Vamos analisar as duas situações:
Tubo sonoro aberto
Seja n o número de nós. Para n = 1, temos o modo mais simples de vibração É o chamado modo fundamental ou primeiro harmônico. Corresponde a um ventre em cada extremidade e entre eles um único nó. Nesta situação a frequência de vibração é denominada frequência fundamental ou frequência do primeiro harmônico.
Sendo L o comprimento do tubo:
Para n = 2 (dois nós entre as extremidades), temos o segundo harmônico.
Nesta situação:
A frequência do segundo harmônico será:
Para o harmônico de ordem n (n nós), teremos:
(n = 1, 2, 3, 4...)
Tubo sonoro fechado
No tubo sonoro fechado temos sempre um ventre na embocadura e um nó na outra extremidade. Na figura representamos o modo mais simples de vibração, constituindo o modo fundamental ou primeiro harmônico. Indicando por n o número de ventres que é igual ao número de nós, temos neste caso n = 1.
A frequência de vibração é a frequência fundamental ou frequência do primeiro harmônico.
Assim, temos:
O segundo modo de vibração do tubo sonoro fechado corresponde a n = 2: dois ventres e dois nós:
 |
| Adicionar legenda |
A frequência desse segundo modo de vibração é igual ao triplo da frequência fundamental, tratando-se, portanto do terceiro harmônico. Assim, para n = 3 teremos o quinto harmônico (2 x 3 - 1); para n = 4, o sétimo harmônico
(2 x 4 - 1). Portanto, o tubo fechado só emite harmônicos de ordem ímpar.
Desse modo, para n nós ou n ventres temos o harmônico de ordem 2n - 1. Neste caso geral, podemos escrever:
n = 1 => 2n - 1 = 1
n = 2 => 2n - 1 = 3
n = 3 => 2n - 1 = 5
n = 4 => 2n - 1 = 7
Exercícios básicos
Exercício 1:
Ondas estacionárias são produzidas numa corda tensa. Sabendo–se que o primeiro harmônico corresponde à corda vibrando com um ventre (n = 1), o segundo harmônico corresponde à corda vibrando com dois ventres (n = 2), represente a corda vibrando no terceiro e no quarto harmônicos e calcule, em cada caso, a frequência de vibração da corda, em função de L e de v.
Resolução: clique aqui
Exercício 2:
Uma corda de com 40 cm de comprimento e 10 gramas de massa, está tracionada por uma força de intensidade 360 N.
a) Qual é a velocidade das ondas que se propagam na corda e que produzem as ondas estacionárias?
b) Qual a frequência fundamental emitida?
Resolução: clique aqui
Exercício 3:
Ondas estacionárias são produzidas num tubo sonoro aberto. Sabendo–se que o primeiro harmônico corresponde ao tubo vibrando com um nó (n = 1), o segundo harmônico corresponde ao tubo vibrando com dois nós (n = 2), represente o tubo vibrando no terceiro harmônico (n = 3) e calcule a frequência de vibração do tubo, em função de L e de v.
Resolução: clique aqui
Exercício 4:
Ondas estacionárias são produzidas num tubo sonoro fechado. Sabendo–se que o primeiro harmônico corresponde ao tubo vibrando com um nó e um ventre (n = 1), o terceiro harmônico corresponde ao tubo vibrando com dois nós e dois ventres
(n = 2), represente o tubo vibrando no quinto harmônico (n = 3) e calcule frequência de vibração do tubo, em função de L e de v.
Resolução: clique aqui
Exercício 5:
Têm-se dois tubos sonoros, um aberto e outro fechado, que emitem a mesma frequência fundamental de 330 Hz. Sabendo-se que o som se propaga no ar com velocidade de 330 m/s, determine os comprimentos de cada tubo.
Resolução: clique aqui
Exercício 6:
Um tubo fechado tem comprimento igual a 50 cm. Ele emite um som de frequência fundamental igual a duas vezes a frequência fundamental do som emitido por um tubo aberto. Ambos são preenchido com ar. Qual é o comprimento do tubo aberto?
Resolução: clique aqui
Exercícios de Revisão
Revisão/Ex 1:
(UFMG)
Bruna afina a corda mi de seu violino, para que ela vibre com uma frequência mínima de 680 Hz.
A parte vibrante das cordas do violino de Bruna mede 35 cm de comprimento, como mostrado nesta figura:
Considerando essas informações,
a) CALCULE a velocidade de propagação de uma onda na corda mi desse violino.
b) Considere que a corda mi esteja vibrando com uma frequência de 680 Hz. DETERMINE o comprimento de onda, no ar, da onda sonora produzida por essa corda.
Velocidade do som no ar = 340 m/s
Resolução: clique aqui
Revisão/Ex 2:
(UFOP)
Assinale a alternativa incorreta.
A) A propagação do som é um fenômeno ondulatório longitudinal que só ocorre em um meio material como, por exemplo, um fluido.
B) Em uma corda vibrante, com as extremidades fixas, o maior comprimento de onda possível para uma onda estacionária é de duas vezes o comprimento da corda.
C) O quadrado da velocidade de propagação da onda em uma corda vibrante é inversamente proporcional à massa da corda.
D) Em um tubo sonoro, de comprimento L, fechado em uma das extremidades, o maior comprimento de onda λ possível para uma onda ressonante é de duas vezes o comprimento do tubo.
Resolução: clique aqui
Revisão/Ex 3:
(UECE)
Duas cordas, M e m, de um violão, estão vibrando em suas respectivas frequências fundamentais.
Sabendo-se que a frequência maior fM está uma oitava acima da frequência menor fm, e que a tensão aplicada às cordas é a mesma, a razão μm/μM entre as densidades lineares das cordas é
A) 2
B) 4
C) 8
D) 16
Revisão/Ex 4:
(Olimpíada Brasileira de Física)
Um músico tem a terceira corda (a “corda Sol”) de seu violão partida. Como no momento ele não dispõe de outra equivalente para substituir, ele resolve então colocar em seu lugar uma segunda corda (a “corda Si”). Sabe-se que a frequência da nota Sol é igual a 4/5 da frequência da nota Si. Identifique a seguir a alternativa que indica por qual fator o músico deve multiplicar a tensão na “corda Si” para que, em vez da nota Si, ela emita a nota Sol como a sua frequência fundamental.
Considere que a densidade da “corda Si” não varia com a tensão.
a) 4/5 b) 16/25 c) 5/4 d) 25/16 e) 2 / 5
Resolução: clique aqui
Revisão/Ex 5:
(UFRJ)
O canal que vai do tímpano à entrada do ouvido pode ser considerado como um tubo cilíndrico de 2,5 cm de comprimento, fechado numa extremidade e aberto na outra. Considere a velocidade do som no ar igual a 340m/s. Calcule a frequência fundamental de vibração da coluna de ar contida nesse canal.
Resolução: clique aqui




















Nenhum comentário:
Postar um comentário