Associação de resistores (II)
Associação em série
Clique para ampliar
Entre os terminais A e B vamos aplicar uma ddp U. É possível substituir toda associação por um só resistor que produz o mesmo efeito. É o resistor equivalente.
Na associação em série:
1) Todos os resistores são percorridos pela mesma intensidade de corrente i, inclusive o equivalente.
2) A ddp em cada resistor é diretamente proporcional à sua resistência elétrica:
xxxxxxxxxxxxxxx U1 = R1.i
xxxxxxxxxxxxxxx U2 = R2.i
xxxxxxxxxxxxxxx U3 = R3.i
3) A potência elétrica dissipada em cada resistor é diretamente proporcional à sua resistência elétrica:
xxxxxxxxxxxxxxx U2 = R2.i
xxxxxxxxxxxxxxx U3 = R3.i
3) A potência elétrica dissipada em cada resistor é diretamente proporcional à sua resistência elétrica:
xxxxxxxxxxxxxxx P1 = R1.i2
xxxxxxxxxxxxxxx P2 = R2.i2
xxxxxxxxxxxxxxx P3 = R3.i2
4) A ddp total é a soma das ddps parciais:
xxxxxxxxxxxxxxx P2 = R2.i2
xxxxxxxxxxxxxxx P3 = R3.i2
4) A ddp total é a soma das ddps parciais:
xxxxxxxxxxxxxxx U = U1 + U2 + U3
5) A resistência equivalente é igual à soma das resistências associadas
5) A resistência equivalente é igual à soma das resistências associadas
xxxxxxxxxxxxxxx RS = R1 + R2 + R3
Clique para ampliar
Na associação em paralelo:
1) Todos os resistores são submetidos à mesma ddp U, inclusive o equivalente.
2) A intensidade da corrente que percorre cada resistor é inversamente proporcional à sua resistência elétrica:
xxxxxxxxxxxxxxx i1 = U/R1xxxxxxxxxxxxxxx i2 = U/R2
xxxxxxxxxxxxxxx i3 = U/R3
3) A potência elétrica dissipada em cada resistor é inversamente proporcional à sua resistência elétrica:
xxxxxxxxxxxxxxx P1 = U2/R1xxxxxxxxxxxxxxx P2 = U2/R2
xxxxxxxxxxxxxxx P3 = U2/R3
4) A intensidade da corrente total é a soma das intensidades das correntes nos resistores associados:
xxxxxxxxxxxxxxx i = i1 + i2 + i3
5) O inverso da resistência equivalente é igual à soma dos inversos das resistências associadas:
xxxxxxxxxxxxxxx 1/Rp = 1/R1 + 1/R2 + 1/R3
Exercícios básicos
Para as associações abaixo (exercícios 1, 2, 3 e 4), calcule a resistência equivalente entre os terminais A e B.
x
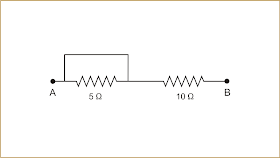
Dica: o resistor de 5 Ω, cujos terminais estão ligados por um fio sem resistência está em curto-circuito. Ele pode ser eliminado do circuito.
Exercício 4:
x
x
Dica: Os pontos A e D, ligados por um fio sem resistência, podem ser considerados coincidentes. O mesmo ocorre com os pontos C e B. Refaça a associação considerando A e D um único ponto, assim como C e B. A seguir, transporte os resistores. Você verá que eles estão ligados em paralelo.
Exercício 5:
Exercício 5:
Considere o circuito abaixo.
Calcule:
a) as intensidades das correntes i, i1 e i2;
b) a potência elétrica dissipada pelo resistor de 8 Ω.
x






Nenhum comentário:
Postar um comentário