13ª aula - 2º semestre
Construção de imagens nas lentes Esféricas Delgadas
Borges e Nicolau
Para as lentes convergentes vamos analisar três posições principais de um objeto:
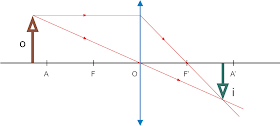
• Objeto colocado antes do ponto anti-principal objeto A:
A imagem é REAL, INVERTIDA E MENOR DO QUE O OBJETO.
Este tipo de imagem é formada nas máquinas fotográficas.
• Objeto colocado entre o ponto anti-principal objeto A e o foco principal objeto F:
A imagem é REAL, INVERTIDA E MAIOR DO QUE O OBJETO.
Este tipo de imagem é formada nos projetores de slides e de filmes.
• Objeto colocado entre o foco principal objeto F e o centro óptico da lente:
A imagem é VIRTUAL, DIREITA E MAIOR DO QUE O OBJETO.
Este tipo de imagem é formada nas lupas (lentes de aumento).
Para as lentes divergentes, qualquer que seja a posição do objeto, a imagem é:
VIRTUAL, DIREITA E MENOR DO QUE O OBJETO
Animação:
Clique
aqui
Exercícios básicos
Exercício 1:
Assinale a proposição correta a respeito da imagem de um objeto linear colocado diante de uma lente esférica delgada :
I) A imagem real é invertida.
II) A imagem virtual é direita.
III) O elemento (objeto ou imagem) de maior altura está mais próximo da lente.
IV) Sendo a imagem virtual a lente é divergente.
Resolução: clique aqui
Exercício 2:
Um objeto linear é colocado diante de uma lente delgada convergente, exatamente sobre o ponto anti-principal objeto A. Sejam F, F’ os focos principais, objeto e imagem e A’ o ponto anti-principal imagem. Dê as características da imagem formada.
Resolução: clique aqui
Exercício 3:
Um objeto linear é colocado diante de uma lente delgada divergente. Afasta-se o objeto da lente. A imagem:
a) Passa de virtual para real
b) Passa de real para virtual
c) Fica maior
d) Fica menor
e) Fica com a mesma altura.
Resolução: clique aqui
Exercício 4:
A imagem da chama de uma vela é vista através de duas lentes L1 e L2.
Pode-se afirmar que:
a) A lente L1 é divergente
b) A lente L2 é convergente
c) A lente L1 é convergente e a chama da vela está colocada entre e o foco principal objeto F e o ponto anti-principal objeto A.
d) A lente L1 é convergente e a chama da vela está colocada entre e o foco principal objeto F e o centro óptico O.
e) A lente L2 é divergente e a chama da vela está colocada entre e o foco principal imagem F' e o centro óptico O.
Resolução: clique aqui
Exercício 5:
Um pequeno retângulo CDGH é colocado diante de uma lente delgada convergente, conforme indica a figura. Obtenha a imagem do retângulo.
Exercícios de Revisão
Revisão/Ex 1:
(UCPe-RGS)
De acordo com a figura abaixo, assinale a opção que caracteriza corretamente a imagem do objeto que se forma do lado direito da lente.
a) Imagem virtual, invertida e menor.
b) Imagem real, invertida e maior.
c) Imagem real, direita e menor.
d) Imagem virtual, direita e maior.
e) Não há formação de imagem, pois o objeto está entre 2f e f.
Resolução: clique aqui
Revisão/Ex 2:
(UFV-MG)
Colocando-se um objeto em frente a uma lente de distância focal f, observa-se que a imagem formada deste objeto é invertida e sua altura é menor que a do objeto. É correto afirmar que:
a) em relação à lente, a imagem formada encontra-se no mesmo lado do objeto.
b) a lente é divergente.
c) a imagem formada é virtual.
d) o objeto deve estar situado entre o foco e a lente.
e) o objeto deve estar situado a uma distância da lente maior que 2f.
Resolução: clique aqui
Revisão/Ex 3:
(UTFPR)
Um objeto é colocado frente ao sistema óptico representado abaixo.
Esboce a imagem formada:
Assinale as alternativas abaixo com V se verdadeira ou F se falsa.
( ) A formação da imagem esquematizada é comum nas câmeras fotográficas.
( ) A imagem é invertida, maior e pode ser projetada num anteparo.
( ) A imagem forma-se geometricamente entre o foco imagem e o ponto antiprincipal.
A sequência correta será:
A) V, F, V
B) V, F, F
C) F, V, F
D) F, F, F
E) V, V, F
Resolução: clique aqui
Revisão/Ex 4:
(Vunesp)
A figura adiante mostra um objeto AB, uma lente divergente L e as posições de seus focos, F' e F.
a) Copie esta figura em seu caderno de respostas. Em seguida, localize a imagem A'B' do objeto fornecida pela lente, traçando a trajetória de, pelo menos, dois raios incidentes, provenientes de A.
b) A imagem obtida é real ou virtual? Justifique sua resposta.
Resolução: clique aqui
Revisão/Ex 5:
(PUC-SP)
No esquema, O é um objeto real e I, a sua imagem virtual, conjugada por uma lente esférica delgada. A partir das informações contidas no texto e na figura, podemos concluir que a lente é:
a) convergente e está entre O e I.
b) convergente e está à direita de I.
c) divergente e está entre O e I.
d) divergente e está à esquerda de O.
e) divergente e está à direita de I.
Resolução: clique aqui